Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 56
Os diâmetros das hastes e são e , respectivamente. Se for aplicada uma carga de ao anel em , determine a tensão normal média em cada haste se .
Passo 1
Fala aí galerinha, tão bem?
Ele quer a tensão média normal em cada uma das hastes, com . Cara, a tensão média normal é dada por
Sendo a força normal na seção e a área da seção. A área da seção para gente seria as áreas das seções transversais das hastes. Como elas são circulares, a área para cada uma delas será a área de um círculo. Mas e ?
Bem, para cada haste vai ser a força atuando em cada haste. Então precisamos encontrar as forças em cada haste. Para isso é bacana começarmos fazendo um diagrama de corpo livre e depois aplicar as equações de equilíbrio.
O DCL será:
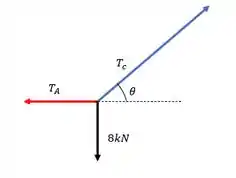
Bora lá!
Passo 2
Vamos come��ar fazendo o equilíbrio das forças na vertical considerando o sentido positivo para cima:
Como
Agora com o equilíbrio dos esforços horizontais, considerando o sentido positivo para a direita:
Substituindo temos:
Com as forças encontradas partimos para as áreas.
Passo 3
Agora, podemos determinar a área circular da seção de cada barra:
Para a haste
Passo 4
Agora, basta fazer a força sobre a área para cada haste
Para a haste
Dica: quando a gente divide algo em (newtons) por algo em , o resultado sai em . Isso pode agilizar nossas continhas, beleza?