Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 1
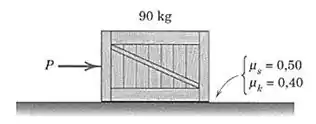
6/1) A força é aplicada ao caixote de , que está em repouso antes que ela seja aplicada . Determine o módulo e a direção da força de atrito exercida pela superfície horizontal sobre o caixote se (a) , (b) e (c) .
Passo 1
Então galera , para que o corpo esteja em equilíbrio , o nosso sistema deve satisfazer o princípio do somatório das forças concorrentes .
Em relação ao eixo , temos que :
Logo ,
Agora que temos a força normal , podemos calcular a força máxima de atrito estático através da relação :
Substituindo os valores que conhecemos :
Passo 2
Agora , analisando o equilíbrio em relação ao eixo :
Logo ,
Para o primeiro caso , temos que :
Sendo assim , como , o bloco não entra em movimento .
A força está na mesma direção porém sentido contrário ao da força , ou seja , para a esquerda .
Passo 3
Para o segundo caso , temos que :
Sendo assim , como , o bloco não entra em movimento .
A força está na mesma direção porém sentido contrário ao da força , ou seja , para a esquerda .
Passo 4
Para o terceiro caso , temos que :
Sendo assim , como , o bloco entra em movimento .
Então , nesse caso , teremos força de atrito cinético , que é dada por :
A força está na mesma direção porém sentido contrário ao da força , ou seja , para a esquerda .
Resposta
Respectivamente ,
Todas para a esquerda!
De boa galera? Então bora resolver mais exercícios como esse!