Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 14

6/14) O homem pesando 80   k g , com centro de gravidade G , suporta o tambor de 34   k g , como mostrado . Ache a maior distância x na qual o homem pode se posicionar sem escorregar , se o coeficiente de atrito estático entre seus sapatos e o chão for de 0,40 .

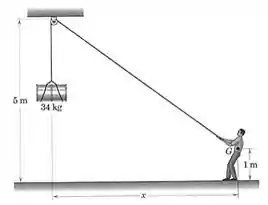
Passo 1

Falaaa! Vamos começar fazendo um DCL, tá bem? Vamos só achar o peso do homem e o peso do tambor:

P H = 9.8 ⋅ 80 = 784   N

P T = 9.8 ⋅ 34 = 333,2   N

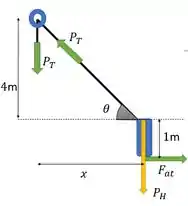
Então, a ideia é a gente pensar: o que acontece quando ele está prestes a escorregar? Ou seja, quando ele está prestes a entrar em movimento?

Temos que o atrito vai ser o atrito estático máximo, certo?

F a t = N ⋅ μ e

Onde μ e = 0,4 e N é a força normal.

Então, o que precisamos fazer, é achar um x onde esse sistema esteja em equilíbrio (esteja paradinho), e que F a t seja o atrito estático máximo. Bora lá!

Passo 2

Vamos começar calculando F a t . N vai ser o peso do homem, porque esse é o valor da força normal do chão sobre ele. Então:

F a t = P H μ e

Como nosso sistema está em equilíbrio, podemos usar as equações do equilíbrio, decompondo nossas forças nos eixos x e y :

∑ F x = 0 → F a t = P T cos ⁡ θ → P H μ e = P T cos ⁡ θ

∑ F y = 0 → P T s e n   θ = P H

Vamos substituir a equação de baixo na de cima:

P T s e n   θ   μ e = P T cos ⁡ θ → s e n   θ   μ e = cos ⁡ θ → t g   θ = 1 μ e

Passo 3

Olhando no desenho, quem é t g   θ ? Concorda que:

t g   θ = 4 x

Da equação do passo anterior:

4 x = 1 μ e ∴ x = 4 μ e = 4 ⋅ 0,4 = 1,6   m

Resposta

x = 1,6   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6/30) A barra uniforme com centro de massa em G é suportada pelas cavilhas A e B que estão presas à roda . Se o coeficiente de atrito entre a barra e as cavilhas é μ , determine o ângulo θ que a roda
6/26) Calcule a força T necessária para girar o carretel de cabo telefônico de 200k g , que se apoia em seu eixo e está enconstado contra uma parede vertical. O coeficiente de atrito dinâmico para cad
6/27) O carro de 1600 kg está começando a subir a rampa de 16 ° . Se o carro tem tração traseira , determine o coeficiente de atrito estático mínimo requerido em B .
6/36) A casca semicil´ndrica de massa m e raio r é girada de um ângulo θ no qual a casca escorrega sobre asuperfície horizontal à medida que P aumenta gradualmente . Que valor de μ s permitirá que θ a
6/31) Um anel de metal com espessura desprezível tem massa m e raio médio r e está pendurado em A . Se o coeficiente de atrito entre o anel e o suporte é μ , determine a força vertical P aplicada à pe