Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 12
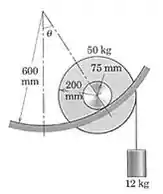
6/12) A roda de rola sobre seu eixo subindo a rampa circular sob a ação do cilindro de preso a um cabo enrolado a sua volta . Determine o ângulo para o qual a roda chega ao repouso , assumindo que o atrito é suficiente para impedir o deslizamento . Qual é o coeficiente de atrito mínimo que permitirá que essa posição seja atingida sem nenhum deslizamento .
Passo 1
Então galera, seja o ponto de contato entre o eixo da roda e a rampa circular .
Como demonstrado nesta seção do livro , temos que :
Sendo assim , para acharmos o valor de , teremos que aplicar a equação de equilíbrio dos momentos em relação a :
Dessa forma ,
Logo ,
Resposta
Tranquilo pessoal? Então partiu resolver mais questões
Exercícios de Livros Relacionados
6/37) O semicilindro homogêneo repousa sobre uma superfície horizontal e estásubmetido a uma força P aplicada a um cabo firmemente preso asua periferia . A força P é lentamente aumentada e mantida nor
6/39) A cabeça do grampo de marceneiro é soldada a seu eixo de diâmetro d e é projetada para prender a peça de trabalho A em seu lugar . O grampo é ajustado batendo inicialmente em sua cabeça com uma
6/40) A garra esquerda móvel de um sargento pode ser deslocada ao longo do conjunto para aumentar a capacidade de pegada do grampo . Para prevenir deslizamento da garra no trilho quando o grampo está
6/50) A embreagem de rotação em miniatura é projetada para permitir que o anel externo gire no sentido horário em relação ao eixo (hachurado) , mas impede rotação no sentido anti-horário . Isso é obti
6/38) Se o coeficiente de atrito entre o cilindro semicircular sólido e o plano inclinado é 0,30 , determine o valor máximo do ângulo θ com a horizontal até o qual o plano pode ser inclinado antes que