Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 147

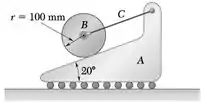
O cilindro B de 3 kg e a cunha A de 2 kg são mantidos em repouso na posição mostrada na figura pela corda C. Considerando que os cilindros rolam sem deslizar sobre a cunha e desprezando o atrito entre a cunha e o solo, determine, imediatamente após a corda C ter sido cortada, (a) a aceleração da cunha, (b) a aceleração angular do cilindro.

Passo 1

Cinemática: Resolvemos aB em aA e um componente paralelo à inclinação

a B = a A + a B / A

Onde a B / A = r α , uma vez que o cilindro rola na cunha A.

a B / A = 0 . 01   m α

Cinética: Cilindro e cunha

→ + Σ F x = Σ F x eff:           0 = m A a A + m B a A - m B a B / A   cos   20 °

0 = 2 + 3 g a A - 3   g 3 12   m α cos ⁡ 20 °

a n = 0.15 cos ⁡ 20 ° α

Passo 2

Cilindro

I - = 1 2 W g r 2 = 1 2 3 g 0 . 01 2

I - = 3 2000 g

Passo 3

b) Aceleração angular do cilindro

+ Σ M E = Σ M E eff:           3 sin ⁡ 20 ° 0 , 01 = I - α + m B a B / A 0 . 0,01 - m B a A cos ⁡ 20 ° 0,01

1.5 sin ⁡ 20 ° = 3 16 9,81 α + 3 9,81 0.25 α 0.25

- 3 9,81 a A cos ⁡ 20 ° 0.25

0.51303 = 0.00582 α + 0.01165 α - 0.04378 a A

Substituindo de (1)

0.51303 = 0.01747 α - 0.04378 0.15 cos ⁡ 20 ° α

0.51303 = 0.01747 - 0.00617 α

α = 45.41   rad/ s 2

Passo 4

a) Aceleração da cunha.

Eq. (1):

a A = 0.15 cos ⁡ 20 ° α

= 0.15 cos ⁡ 20 ° 45.41

a A = 6.401   m / s 2

Resposta

b )   α = 45.4   rad/ s 2  

a )   a A = 6.40 m / s 2 →

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O obturador mostrado na figura foi formado removendo-se um quarto de um disco de 20 mm de raio e é usado para interromper um feixe de luz emitido a partir de uma lente em C. Sabendo que o obturador te
O objeto ABC consiste de duas barras esbeltas soldadas no ponto B.A barra AB tem uma massa de 1 kg e a barra BC tem uma massa de 2 kg. Sabendo que a intensidade da velocidade angular de ABC é 10 rad /
Um cone delgado uniforme de massa m pode balançar livrementeem torno da barra horizontal AB. Se o cone é liberado do repouso naposição mostrada na figura, determine (a) a aceleração da ponta D, (b) a
Uma barra delgada AB de 4 kg e uma barra delgada BC de 2,5 kg estão ligadas por um pino B e por uma corda AC. O conjunto gira em um plano vertical sob o efeito combinado da gravidade e do binário M ap
Desenhe os diagramas de cisalhamento e momento fletor para a viga do Problema 16.84 imediatamente após a quebra do cabo em B.