Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 45
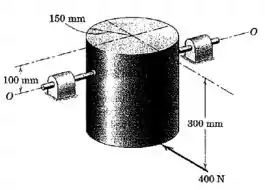
O cilindro maciço homogêneo tem uma massa de e está livre para girar em torno do eixo horizontal -. Se o cilindro, inicialmente em repouso, recebe a ação da força de mostrada, calcule a componente horizontal da força suportada por cada um dos dois mancais, simetricamente colocados, quando a força de é aplicada pela primeira vez.
Passo 1
Se calcularmos o momento resultante sobre o cilindro em relação ao eixo , a única força que terá momento diferente de zero será a de , então:
Podemos usar isso para calcular a aceleração angular . Antes precisamos aplicar o teorema dos eixos paralelos para encontrar o momento de inércia em relação a esse eixo.
Se tivéssemoss um eixo paralelo ao eixo , mas passando pelo centro de massa, poderíamos consultar uma tabela para encontrar o seguinte momento de inércia:
O cilindro tem de altura, então o centro de massa estaria a do topo. Como o eixo está a do topo, a distância entre os dois é:
Então:
Passo 2
E agora podemos usar isso para calcular a aceleração angular:
Então, no instante em que a força de é aplicada, a aceleração do centro de massa do cilindro na direção tangencial ao movimento é:
Onde é a distância entre o eixo de rotação e o centro de massa, que já até calculamos:
E então, pela segunda lei de Newton:
E as forças que agem nessa direção são o peso e as forças horizontais em cada mancal:
Resposta
A força suportada por cada mancal é .