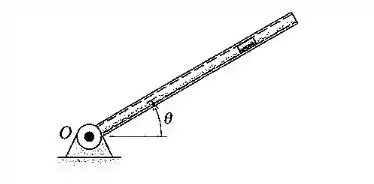
3/57) O tubo vazado em torno do eixo horizontal que passa pelo ponto O e girano plano vertical com umavelocidade angular constante no sentido anti-horário θ ' = 3 r a d / s . Se uma partícula de 0,1k g está deslizando no tubo em direção a O com uma velocidade de 1,2 m / s em relação ao tubo quando a posição θ = 30 ° é ultrapassada , calcule o módulo da forçanormal N exercida pela parede do tubo sobre a partícula neste instante .

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 57

3/57) O tubo vazado em torno do eixo horizontal que passa pelo ponto e girano plano vertical com umavelocidade angular constante no sentido anti-horário . Se uma partícula de está deslizando no tubo em direção a com uma velocidade de em relação ao tubo quando a posição é ultrapassada , calcule o módulo da forçanormal exercida pela parede do tubo sobre a partícula neste instante .

Passo 1

Então pessoal , para resolvermos esse tipo de questão usaremos um raciocínio parecido ao das últimas questões . A principal diferença é que vamos aplicar a análise das forças que atuam sobre um corpo provocando variação nasua velocidade angular ao invés da tangencial . Temos que :

Convém lembrar do capítulo anterior que :

Sabemos que , sendo assim :

Resposta

Tranquilo pessoal? Então partiu resolver mais questões

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a altitude h (em quilômetros) acima da superfície da Terra na qual um satélite em uma órbita circular tem o mesmo período, 23,9344h , que a rotação absoluta da Terra. Se tal órbita se situa

Os discos A e B pesam 30 lb e 12 lb, respectivamente, e um pequeno bloco C de 5 lb está preso à borda do disco B. Supondo que nenhum deslizamento ocorra entre os discos, determine o período de pequena

Façamos a suposição (não realista) de que um barco de massa m, movendo-se com velocidade inicial v0 na água, tenha sua velocidade reduzida por uma força de retardo viscosa de magnitude bv2, onde b é u

Efetue os cálculos numéricos do Exemplo 2.7 para os valores fornecidos na Figura 2.8. Elabore os gráficos das Figuras 2.8 e 2.9. Não duplique a solução no Apêndice H: Elabore a sua própria solução.Exe

Quais das forças a seguir são conservativas? No caso de serem conservativas, determine a energia potencial U(r).Fx = ayz + bx + c, Fy = axz + bz, Fz = axy + by.Fx = -ze-x, Fy = ln z, Fz = e-x + y/z.F