Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 8.Problemas - Ex. 86
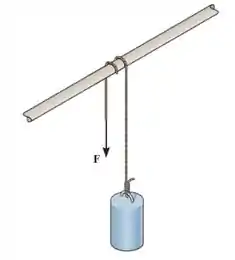
Um cilindro de massa deve ser suportado pela corda que envolve o cano. Determine a maior força vertical que pode ser aplicada à corda sem mover o cilindro. A corda passa (a) uma vez pelo cano, e (b) duas vezes pelo cano . Considere .
Passo 1
Galera, puxar o cilindro que tem um peso faz com que a corda se mova sobre o cano. Na letra (a) queremos saber o maior valor de que pode ser aplicado à corda sem que o cilindro se mova, com . Em radianos, o valor de beta passa a ser . Assim, podemos fazer o uso da seguinte equação
Seja e . Assim, vale:
Passo 2
Agora, na letra (b), queremos saber o maior valor de que pode ser aplicado à corda sem que o cilindro se mova, com . Vamos passar beta para radianos, beleza?
Se valem , valerá . Assim, aplicando na equação os valores, temos:
Resposta
- ;
- .