Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas - Ex. 41

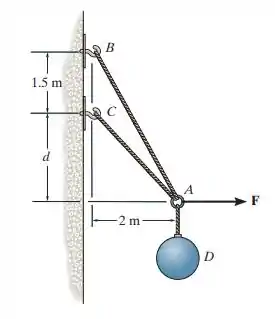
3.19. A esfera D possui uma massa de 20   k g . Se uma força F = 100   N é aplicada horizontalmente no anel em A, determine a dimensão d, de modo que a força no cabo AC seja zero.

Passo 1

O exercício pede para determinar a dimensão d para que a força resultante no cabo AC seja 0, a distância d está relacionada com o ângulo entre a força que age no cabo e os eixos cartesianos, nós temos que achar esse ângulo para determinar d.

Vamos usar a seguinte estratégia, vamos determinar a força resultante no ponto A, assim poderemos determinar F A B , consequentemente vamos ter uma relação entre o ângulo e a distância de F A B .

Passo 2

Vamos começar calculando F R x .

F R x = 100 - F A B ⋅ cos ⁡ θ = 0

Então

100 = F A B ⋅ cos ⁡ θ

Agora vamos fazer o mesmo para F R y . Lembrando de considerar g = 9,81 m / s 2

F R y = F A B ⋅ sin ⁡ θ - 20 ⋅ g = F A B ⋅ sin ⁡ θ - 196,2 = 0

F A B ⋅ sin ⁡ θ = 196,2

Passo 3

Agora temos duas incógnitas e duas equações, vamos resolva-las.

F A B ⋅ cos ⁡ θ = 100

F A B ⋅ sin ⁡ θ = 196,2

Vamos começar elevando ambas as equações ao quadrado e somando para sumir com θ

F A B 2 ⋅ cos 2 ⁡ θ + F A B 2 ⋅ sin 2 ⁡ θ = 100 2 + 196,2 2

F A B 2 ⋅ ( cos 2 ⁡ θ + sin 2 ⁡ θ ) = 48494,44

F A B = 48494,44 = 220,21  

Passo 4

Agora podemos resolver para θ

F A B ⋅ cos ⁡ θ = 100

220,21 ⋅ cos ⁡ θ = 100

θ = c o s - 1 100 220,21 = 62,99 °

Passo 5

O ângulo que a gente obteve foi o seguinte

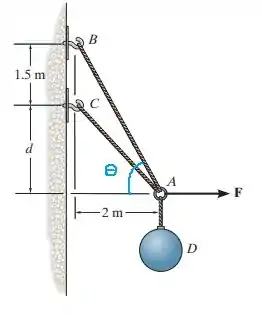
Vamos extrair o seguinte triângulo dessa imagem

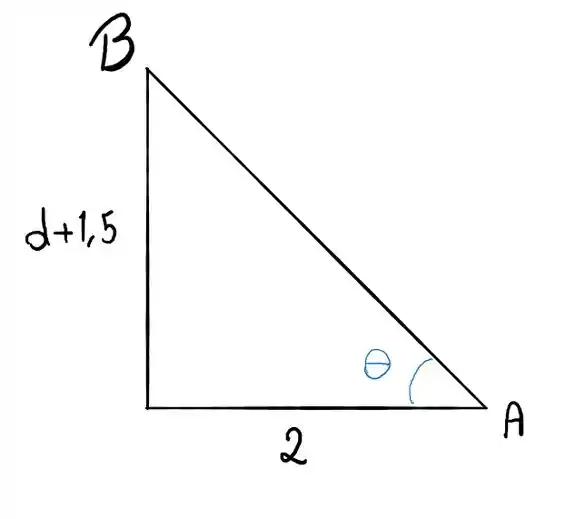
Podemos tirar o valor da tangente de θ lembrando da seguinte relação

tan ⁡ θ = c a t e t o   o p o s t o c a t e t o   a d j a c e n t e = d + 1,5 2

Então

2 ⋅ tan ⁡ 62,99 ° - 1,5 = d

d = 2,42

Resposta

d = 2,42   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Que força de módulo T deve a pessoa aplicar no cabo, para fazer com que a leitura na balança A seja de 2000N ? Os pesos das polias e cabos são desprezíveis. Descreva qualquer hipótese feita.
Um lenhador deseja fazer o tronco da árvore cair para cima do morro, apesar do tronco estar inclinado para baixo. Com a ajuda do guincho W , qual será a força trativa T necessária no cabo? O tronco de
A ferramenta mostrada é projetada para ajudar a remover tampas de latas com argolas. Se o usuário exerce uma força de 40N em A , determine a força trativa T na parte B C da argola.
O poste uniforme com 15m de comprimento tem uma massa de 150k g e está apoiado em suas extremidades lisas contra as paredes verticais e sustentado pela força trativa T do cabo vertical. Calcule as rea
Um tubo P está sendo curvado pela calandra de tubos, como mostrado. Se o cilindro hidráulico aplica uma força com módulo F = 24k N ao tubo em C , determine o módulo das reações dos roletes em A e B .