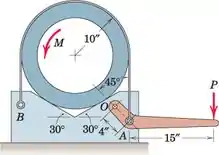
Para o projeto do freio de banda mostrado, encontre o acoplamento M necessário para virar o tubo no bloco em V contra a ação da banda flexível. Uma força P = 25 lb é aplicada à alavanca, que é articulada em torno de O. O coeficiente de atrito entre a faixa e o tubo é de 0,30, e o entre o tubo e o bloco é de 0,40. Os pesos das peças são desprezíveis.
Passo 1
Primeiro, vamos isolar o diagrama de corpo livre da alavanca
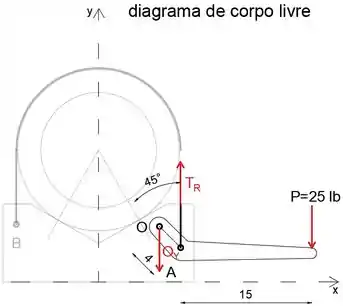
Ao igualar a soma dos momentos sobre o ponto O a zero, podemos determinar a tensão TR
Passo 2
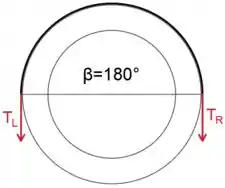
Observe que o acoplamento M é anti-horário e inicia a rotação do tubo contra a ação da banda, o que significa que o tubo gira inicialmente no sentido horário, ou seja, a tensão TR é maior que TL
Sabendo disso, podemos escrever uma expressão para TL como
Vamos substituir TR, e por seus valores
Passo 3
A seguir, vamos isolar o tubo com o par M, as forças de reação em C e D e as tensões TL e TR atuando nele
Observe que o peso do tubo é insignificante
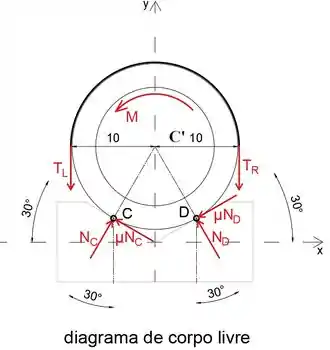
Equacionando a soma das forças na direção x a zero, determinaremos a relação entre NC e ND
Vamos substituir por seu valor
Passo 4
Uma vez que determinamos a relação entre as forças de reação normais, igualando a soma das forças na direção y a zero, podemos determinar seus valores
Vamos substituir por seu valor
A seguir, substituiremos NC pela expressão (1), enquanto as tensões TL e TR serão substituídas por seus valores
Passo 5
Vamos colocar o valor de ND na equação (1) a fim de determinar NC
Finalmente, ao igualar a soma dos momentos sobre o centro C'a zero, determinaremos o par M
Coloque todos os valores conhecidos na equação acima