Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 110
Repita Prob. 6/109, só agora os coeficientes de atrito estático são os seguintes: 0,60 em A e C e 0,20 em B. Plote T/mg como uma função de y para , onde r é o raio comum de todos os três veios. Quais são os valores limites de T/mg para y = 0 e para grandes valores de y?
Passo 1
Como estamos tentando levantar o cilindro, sabemos que a tensão T é maior que o peso W, sabendo que o coeficiente de atrito não é igual para todas as superfícies, podemos escrever a expressão para a tensão T como
Desde a
Passo 2
E uma vez que sabemos que W = mg, podemos escrever a expressão acima como
No esboço abaixo, podemos ver que os ângulos , e são
Passo 3
Portanto, a expressão para a tensão T agora será semelhante a esta
Também podemos escrever esta expressão como
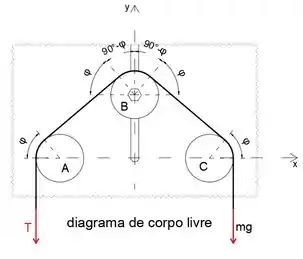
Passo 4
Uma vez que a linha FE é tangente a ambos os círculos, ABEF é um retângulo
Sabendo disso, sabemos que os lados dos ângulos e são perpendiculares, o que significa que os ângulos são iguais
Do triângulo AOB podemos facilmente determinar o ângulo , ou seja, o ângulo
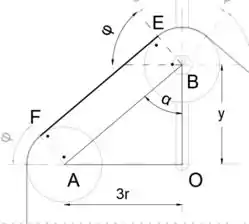
Passo 5
Agora podemos substituir o ângulo na equação (1) pela expressão (2)
Da expressão acima, podemos escrever T/mg como
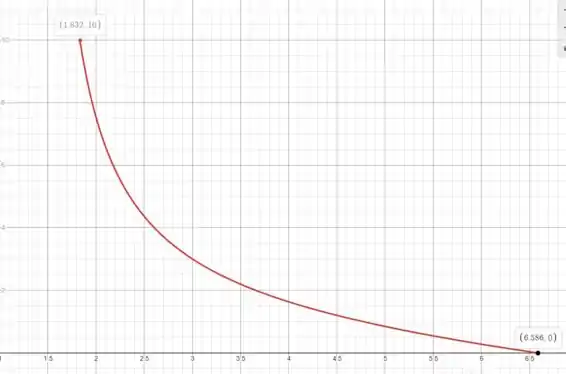
Usando uma calculadora gráfica como o Desmos (link nos comentários), traçaremos esta função
Podemos ver que o valor máximo é
Embora o valor mínimo seja
