Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 135

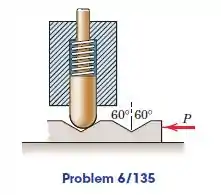
O mecanismo de detenção consiste em molas êmbolo com uma extremidade esférica, que é projetado para posicionar a barra horizontal, engatando os entalhes espaçados. Se a mola exercer uma força de 40   N sobre o êmbolo na posição mostrada e uma força P = 60   N é necessário mover a barra de retenção contra o êmbolo, calcule o coeficiente de fricção entre o êmbolo e o detentor. É conhecido testes anteriores que o coeficiente de atrito entre a barra de luz e a superfície horizontal é de 0,30 . Presumir que o êmbolo está bem lubrificado e com precisão encaixado de modo que o atrito entre ele e seu guia seja insignificante.

Passo 1

Precisamos de uma expressão para T que represente a subida e a descida da caixa.

O coeficiente mínimo de atrito entre o cabo e a polia é dado por:

ln ⁡ T 2 T 1 = μ β

Ou:

T 2 T 1 = e μ β

Onde T 1 é a tensão na corda no lado tenso e T 2 no lado frouxo.

Substituindo os respectivos valores, temos que:

T T 1 = e μ β

T 1 = T e - μ β

Passo 2

Para levantar o peso, temos que a condição de trabalho deve ser:

T sen ⁡ θ + T 1 sen ⁡ θ = m g

Substituindo os dados, temos que:

T sen ⁡ θ + T e - μ β sen ⁡ θ = m g

T = m g sen ⁡ θ 1 + e - μ β

Passo 3

No momento da descida, a ordem das tensões é invertida, e T representa o lado frouxo, logo:

T 1 T = e μ β

Realizando o mesmo procedimento do passo anterior, temos que:

T sen ⁡ θ - T 1 sen ⁡ θ = m g

Substituindo os dados, temos que:

T sen ⁡ θ - T e μ β sen ⁡ θ = m g

T = m g sen ⁡ θ 1 - e μ β

Resposta

  1. T = m g sen ⁡ θ 1 + e - μ β

  2. T = m g sen ⁡ θ 1 - e μ β
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a magnitude e a direção da força de atrito que a parede vertical exerce no bloco de 100l b se ( a )θ = 15 ° e ( b )θ = 30 ° .
As pinças são projetadas para lidar com tubos de aço quente que estão sendo tratados termicamente em banho de óleo. Para uma abertura de mandíbula de 20 ° , qual é o coeficiente mínimo de atrito estát
A magnitude da força P é aumentada lentamente. A caixa homogênea de massa m desliza ou tomba primeiro? Indique o valor de P que causaria cada ocorrência. Negligencie qualquer efeito do tamanho dos pés
A força 700N é aplicada ao bloco de 100k g , que fica estacionário antes de a força ser aplicada. Determine a magnitude e a direção da força de atrito F exercida pela superfície horizontal no bloco.
Determine o coeficiente mínimo de atrito estático μ s que permitirá que o tambor com cubo interno fixo seja enrolado na inclinação de 15 ° a uma velocidade constante sem escorregar. Quais são os valor