Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 2
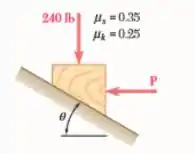
Determine se o bloco mostrado está em equilíbrio e encontre a magnitude e a direção da força de atrito quando e .
Passo 1
Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente determine se o bloco está ou não em equilíbrio e o atrito dado e . Para isso, devemos utilizar as formulas de equilíbrio assumindo que o corpo está em repouso. Porém, precisamos primeiro decompor a força P e a força de . Fica assim:
Para :
Passo 2
Agora, para encontrarmos o atrito máximo, devemos utilizar a seguinte fórmula:
Como a força é maior que a máxima podemos concluir que o bloco está descendo.
A magnitude da força peso, será:
Resposta
Como a força é maior que a máxima podemos concluir que o bloco está descendo.
Exercícios de Livros Relacionados
Um vagão ferroviário tem massa 30M g e é apoiado em oito rodas de 800m m de diâmetro, com eixos de 125m m de diâmetro. Sabendo que os coeficientes de atrito são μ s = 0,020 e μ k = 0,015 , determine a
Resolva o Problema 8.10 8 supondo que a correia plana e os tambores sejam substituídos por uma correia em V e por polias em V com α = 36 ° . (O ângulo α é mostrado na Fig. 8.15 a .)
Resolva o Problema 8.126 considerando que θ = 75 ° .
Complete a dedução da Eq. 8.15 que relaciona as trações nas duas partes de uma correia em V .
Resolva o Problema 8.122 considerando que o tambor esticador C esteja fixo e não possa girar.