Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 18

O cilindro mostrado na figura tem peso W e raio r. Expresse, em termos de W e r, a intensidae do maior binário M que pode ser aplicado ao cilindro para que ele não gire, considerando que o coeficiente de atrito estático seja ( a ) zero em A e 0,3 em B, ( b ) 0,25 em A e 0,3 em B.

Passo 1

Beleza! Vamos começar esse excercício desenhando o DCL do cilindro quando estamos na iminência do movimento, então:

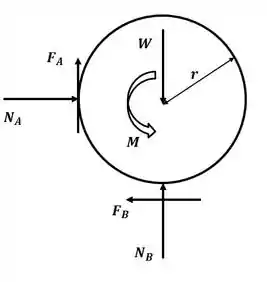
Dessa forma, na iminência do movimento, temos as forças de atrito estático em A e B dadas por:

F A = μ A N A

F B = μ B N B

Passo 2

Agora vamos aplicar o somatório de forças na direção x :

+ → ∑ F x = 0

N A - F B = 0 → N A = F B = μ B N B

Isolando N A da equação obtida no passo 1, temos:

N A = F A μ A

Substituindo esse valor na equação anterior:

F A μ A = μ B N B → F A = μ A μ B N B

Agora vamos aplicar o somatório de forças na direção y :

+ ↑ ∑ F y = 0

N B + F A - W = 0

Substituindo o valor encontrado para F A :

N B + μ A μ B N B = W → 1 + μ A μ B N B = W → N B = W 1 + μ A μ B

Passo 3

Subsituindo esse valor de N B encontrado na equação do passo 1, temos:

F B = μ B N B → F B = μ B W 1 + μ A μ B

E agora susbtituindo o valor de N B na equação para F A :

F A = μ A μ B N B → F A = μ A μ B W 1 + μ A μ B

Agora, aplicando o somatório de momento em relação ao centro do cilindro, temos:

+ ↺ ∑ M C = 0

M - F A r - F B r = 0 → M = r F A + F B

Agora, substituindo os valores encontrados para F A e F B :

M = r μ A μ B W 1 + μ A μ B + μ B W 1 + μ A μ B → M = r μ B W 1 + μ A 1 + μ A μ B

Agora, substituindo os valores para a letra ( a ) μ A = 0 e μ B = 0,3 :

M = r 0,3 W 1 + 0 1 + 0 0,3 → M = 0,3 r W

Agora, substituindo os valores para a letra ( b ) μ A = 0 , 25 e μ B = 0,3 :

M = r 0,3 W 1 + 0,25 1 + 0 , 25 0,3 → M = 0,35 r W

Resposta

M = 0,3 r W

M = 0,35 r W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6/15) O painel vertical de 800k g tem centro de massa em G . O painel é montado sobre rodas que permitem facilidade de movimento horizontal ao longo do trilho fixo . Se o mancal da roda em A trava , d
6/22) O sistema de dois blocos , cabo e polia fixaestá incialmente em repouso . Determine a força horizontal P necessária para causar movimento quando (a) P é aplicada ao bloco de 5k g e (b) P é aplic
6/16) Determine a força horizontal P necessária para causar deslizamento . Os coeficientes de atrito para os três pares de superfícies em contato estão indicados . O bloco superior é livre para se mov
6/25) Que força P os dois homens devem exercer na corda para deslizar a prancha uniforme de 6m sobre os suportes suspensos? A prancha tem massa de 100k g e o coeficiente de atrito dinâmico entre a pra
6/18) A barra uniforme A B de massa m e comprimento l está apoiada contra a parede vertical como mostrado . O coeficiente de atrito estático entre as superfícies de apoio e as extremidades da barra é