6/15) O painel vertical de tem centro de massa em . O painel é montado sobre rodas que permitem facilidade de movimento horizontal ao longo do trilho fixo . Se o mancal da roda em trava , de forma que a roda não possa girar , calcule a força necessária para deslizar o painel . O coeficiente de atrito dinâmico entre a roda e o trilho vale .
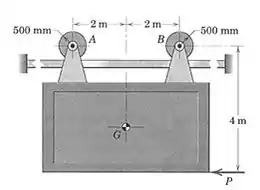
Passo 1
Então galera , seja o ponto localizado na base do painel vertical e com a mesma localização horizontal do centro da polia , e a força vertical aplicada no centro da polia .
Dessa forma , aplicando a equação do equílibrio do momento em , temos que :
Logo ,
Passo 2
Bom pessoal , agora para resolvermos este exercício basta aplicarmos a equação do equilíbrio do sistema :
Sendo assim ,
Resposta
Suave galera? Então bora próxima!!!