Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 44
Determine o ângulo pelo qual a extremidade A gira quando mm,mm,mm, GPa e .
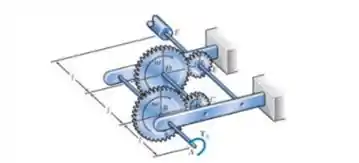
Passo 1
E ai gurizada tudo belezinha? Pessoal para resolvermos esta questão usamos a fórmula abaixo para encontrarmos o ângulo do giro em A, seguindo ela é bem simples de resolvermos, então vem comigo:
Considerando os seguintes dados temos:
Precisamos encontrar o valor do momento de inércia para prosseguirmos:
Agora sim podemos determinar o ângulo de rotação :D
Resposta
Exercícios de Livros Relacionados
O motor transmite 33k W ao eixo de aço inoxidável 304 quando gira a 20H z . O eixo tem diâmetro de 37,5m m e está apoiado em mancais lisos em A e B , que permitem a livre rotação do eixo. As engrenage
O motor transmite 33k W ao eixo de aço inoxidável 304 quando gira a 20H z . O eixo é apoiado em mancais lisos em A e B , que permitem a livre rotação do eixo. As engrenagens C e D presas ao eixo absor
Um diagrama tensão-deformação por cisalhamento para um eixo maciço de 50 mm de diâmetro pode ser aproximado como mostra a figura. Determine o torque exigido para provocar uma tensão de cisalhamento má
O eixo cônico é feito de liga de alumínio 2014-T6 e seu raio pode ser descrito pela função r = 0,02 ( 1 + x 3 / 2 ) m , onde x é dado em metros. Determine o ângulo de torção de sua extremidade A se el
Os eixos de 30m m de diâmetro são feitos de aço-ferramenta L2 e estão apoiados em mancais que permitem aos eixos girarem livremente. Se o motor em A desenvolver um torque T =45N . m no eixo A B , enqu