Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 95
O eixo de aço doce mostrado na figura é considerado elastoplástico com e .Determine a máxima tensão de cisalhamento e o raio do núcleo elástico causado pela aplicação de um torque de intensidade (a) e (b)
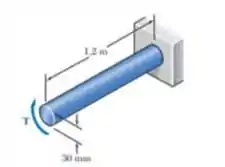
Passo 1
E ai gurizada tudo belezinha? O enunciado pede que a determine a máxima tensão de cisalhamento e o raio do núcleo elástico causado pela aplicação de um torque de intensidade (a) e (b)
Muito bem gurizada, vamos calcular (a) primeiramente:
desde que o eixo será elástico.
Agora a tensão máxima de cisalhamento é determinada como:
Substituindo os valores temos:
Agora vamos ao raio do núcleo elástico de (a):
Passo 2
Agora turma, vamos para o cálculo do (b):
desde que o eixo será elástico.
Vamos ver a tensão máxima de cisalhamento de (b):
Vamos ao raio do núcleo elástico de (b):
Resposta
- e