Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 41
Dois eixos, cada um com diâmetros de, são conectados pelas engrenagens mostradas na figura. Sabendo que e que o eixo está fixo em F , determine o ângulo pelo qual a extremidade A gira quando lhe é aplicado um torque de
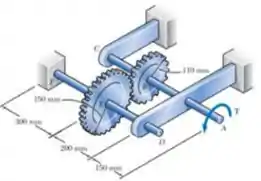
Passo 1
E aí gurizada tudo belezinha? Espero que sim!! Então vamos começar calculando cada trecho de torque
A força de contato entre as engrenagens B e E pode ser determinada através da relação torque e raio de cada seção :D
Considerando o torque da seção AB temos:
Passo 2
Agora temos que determinar a torção no eixo FE. Considerando os seguintes dados temos:
Agora temos que determinar a angolatura vem comigo :D
Passo 3
E a rotação em E é determinada tal como:
O deslocamento tangencial na engrenagem é dado por:
E A rotação em B é dada por:
Para determinarmos a torção no eixo BA, consideramos os seguintes dados:
Calculando o ângulo da seção A/B temos:
Ufaaaaa agora sim podemos determinar a rotação em A:
Resposta
Então gurizada, conseguimos determinar que a extremidade de A gira em .