Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 8
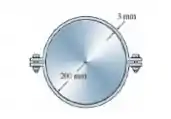
A cinta de aço A-36 tem 50 mm de largura e está presa ao redor do cilindro rígido. Se os parafusos forem apertados de modo que a tração neles seja 2 kN, determine a tensão normal na cinta, a pressão exercida sobre o cilindro e a distância até onde metade da cinta estica.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que a nossa cinta tem paredes com 3mm de espessura e 200 mm de raio interno, além de que recebe uma tração de 2kN quando seus parafusos são bem apertados. Depois de falar isso tudo, ele nos pede tensão nas paredes, pressão sobre o cilindro e a distância até a cinta estica metade dela. Viu?? Nem é tão difícil assim. Bora lá fazer?? Partiu??!!
Passo 2
Nas questões de vasos cilíndricos de paredes finas, temos duas tensões normais: σ1 (na direção circunferencial, ou seja, do aro) e σ2 (no sentido longitudinal, ou seja, axial). No nosso caso, sabemos que, como a extremidade é livre, não teremos a tensão axial, apenas a circunferencial.
Então, podemos afirmar que as nossas tensões serão:
Passo 3
Sendo assim, achamos que a tensão será:
Como a cinta está sujeita a uma tração de , e possui de largura por de espessura, teremos que a tensão normal será:
Logo:
Agora a pressão será dada como:
Sendo assim:
E por fim, a distância até onde metade da cinta estica será dada como:
Onde será:
Portanto: