Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 8.Problemas - Ex. 32
Se o coeficiente de atrito estático entre a caixa de e o piso é , enquanto o coeficiente de atrito estático entre os sapatos do homem de e o piso é . Determine se o homem pode mover a caixa.
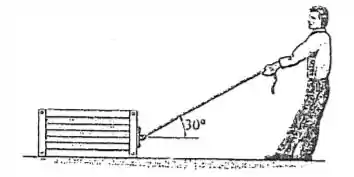
Passo 1
Com base nas informações fornecidas pelo enunciado, desejamos descobrir se o homem conseguirá mover a caixa. Vamos tomar então os seguintes diagramas de forças
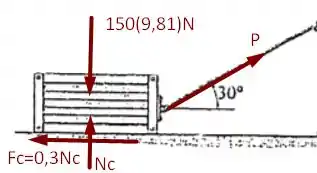
Diagrama de forças para a caixa;
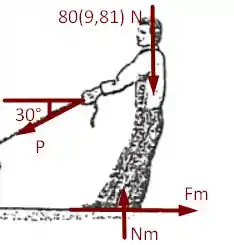
Diagrama de forças para o homem;
Passo 2
A partir dos diagramas acima, podemos utilizar as equações do equilíbrio e vamos obter
Resolvendo o sistema composto pelas equações encontramos
Passo 3
Com o resultado acima podemos nos basear no diagrama de forças da caixa e tomar as seguintes equações
Como temos o valor de vamos comparar com o valor máximo que o homem suporta sem escorregar que é dado por
Tendo que o homem não escorrega e, portanto, consegue deslocar a caixa.
Resposta
O homem pode mover a caixa.