Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 48

Dois blocos A e B, cada um com massa de 5   k g , estão conectados pela estrutura mostrada. Se o coeficiente de atrito estático nas superfícies de contato é u = 0,5 , determine a maior força P que pode ser aplicada ao pino C da estrutura sem fazer com que os blocos se movam. Desconsidere o peso da estrutura.

Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

Primeiramente, a componente das forças paralela à superfície no ponto de contato do bloco com o chão deve ser menor que a força de atrito. Pegando o bloco A:

F a t   A = 5 × 10 × 0,5 = 25   N

Para o bloco B :

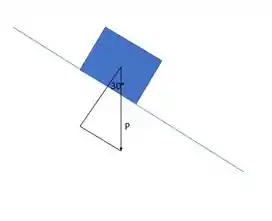
Neste caso, a força normal será:

N = P c o s 30 °

Logo, o atrito será:

F a t   B = 25 cos ⁡ 30 ° × 0,5 = 10,82   N

Passo 2

Agora, basta calcular as componentes paralelas à superfície em cada bloco e comparar com a força de atrito em cada um deles. Pegando o bloco A ,   a força horizontal que atua nele será:

P s e n 30 ° = F a t   A

P = 25 s e n 30 ° = 50   N

Esta é a força máxima que pode ser aplicada para que o bloco A   não se mova.

Passo 3

Agora, pegando o bloco B ,   devemos achar a força que atua paralelamente à superfície, sabemos que:

Decompondo novamente na componente paralela à superfície:

P s e n 30 ° × cos ⁡ 30 ° = F a t   B

P = 24,98   N

Por fim, devemos escolher o menor valor de P   encontrado como a força máxima a ser aplicada, pois, se pegarmos o maior valor de P ,   o bloco com a menor força de atrito vai andar. Logo:

P m á x = 24,98   N

Resposta

P m á x = 24,98   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se os coeficientes de atrito estático nos pontos de contato A e B são μ s = 0,4 e μ s ' = 0,2 , respectivamente, determine a menor força P que fará com que o carrretel de 150k g tenha iminência de mov
Se o coeficiente de atrito estático entre a caixa de 150 k g e o piso é μ s = 0,3 , determine o menor coeficiente de atrito estático entre os sapatos do homem e o piso de modo que o homem possa mover
Se o coeficiente de atrito estático entre a caixa de 150 k g e o piso é μ s = 0,3 , enquanto o coeficiente de atrito estático entre os sapatos do homem de 80 k g e o piso é μ s ' = 0,4 . Determine se
O disco de 45 k g se apoia sobre a superfície para a qual o coeficiente de atrito estático μ s = 0,2 . Determine o maior momento de binário M que pode ser aplicado à barra sem causar movimento.
O utilitário com tração nas quatro rodas de 3M g tem centro de massa em G . Determine a massa máxima da tora que pode ser rebocada pelo automóvel. O coeficiente de atrito estático entre a tora e o sol