Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 81
O bloco e o equipamento mostrados são usados para elevar uma carga de 150 lb. Cada uma das polias de 3 pol. De diâmetro gira em um eixo de 0,5 pol. Sabendo que o coeficiente de atrito estático é 0,20, determine a tensão em cada parte do cabo à medida que a carga é aumentada lentamente.
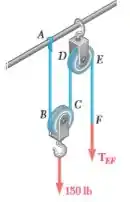
Passo 1
Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente determine a tensão em cada parte do cabo à medida que a carga é aumentada lentamente. Para isso:
Passo 2
Agora, precisamos utilizar as formulas de momento e equilíbrio nas polias:
Para as forças no eixo , temos:
Por fim, temos:
Resposta
Exercícios de Livros Relacionados
Resolva o Problema 8.32 considerando que o diâmetro do tubo é 30 mm.
Um tubo de 60 mm de diâmetro é apertado pela chave inglesa mostrada na figura. As partes AB e DE da chave são rigidamente ligadas entre si e a parte CF é conectada por um pino em D. Se a chave deve ap
Sabendo que o coeficiente de atrito estático entre o colar e a barra é 0,35, determine o intervalo dos valores de P para que o equilíbrio seja mantido quando θ = 50 ° e M = 20N . m .
Dois blocos A e B de 4,5 N estão ligados por uma haste esbelta de massa desprezível. O coeficiente de atrito estático é 0,30 entre todas as superfícies de contato, e a barra forma um ângulo θ = 30 ° c
Sabendo que o coeficiente de atrito estático entre o colar e a barra é 0,40, determine o intervalo dos valores de M para que o equilíbrio seja mantido quando θ = 6 0 ° e P = 200N .