Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 93
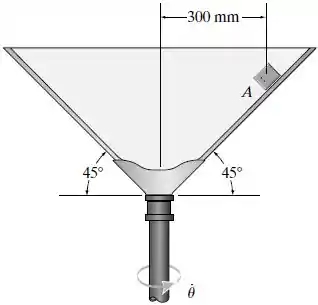
Se o coeficiente de atrito estático entre a superfície cônica e o bloco de massa é , determine a velocidade angular constante máxima sem fazer com que o bloco escorregue para cima.
Passo 1
O enunciado nos dá as seguintes informações:
Massa do bloco:
Coeficiente de atrito estático:
:
O enunciado pede para determinarmos a velocidade angular constante máxima para que o bloco não escorregue para cima. Essa condição faz com que a gente tenha uma força de atrito na mesma direção, porém com sentido oposto à esse movimento. Sabemos que a fórmula para a força de atrito é dada por
O diagrama de corpo livre ilustra essa situação.
Onde é a força peso, e é a força normal exercida pela superfície.
Passo 2
Primeiramente, vamos encontrar as derivadas temporais.
Como o bloco não pode escorregar, os valores de e de serão constantes, ou seja, não irão variar no tempo. Logo
Além disso, também sabemos que é constante, logo
Passo 3
Sabemos que as componentes da aceleração do bloco nas coordenadas , e são dadas por
Logo,
Passo 4
Agora aplicaremos as Equações do Movimento.
Analisando primeiramente no eixo , temos
Sabemos que . Substituindo esse valor na equação acima, obtemos
Analisando no eixo , temos que
Portanto, a velocidade angular constante máxima será