Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 109
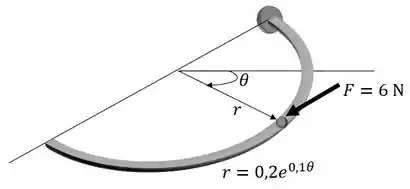
Utilizando a pressão do ar, a bola de 0,5 kg é forçada a se mover por um tubo colocado no plano horizontal com o formato de uma espiral logarítmica. Se a força tangencial exercida sobre a bola devida à pressão do ar é de 6 N, determine a taxa de aumento na velocidade da bola no instante . Também, qual é o ângulo da coordenada radial deformada até a linha de ação da força de 6 N?
Passo 1
O Problema nos deu as seguintes informações:
Massa da bola:
Força tangencial:
Movimento no plano horizontal.
A questão pede para determinarmos a taxa de aumento na velocidade da bola no instante e o o ângulo da coordenada radial deformada até a linha de ação da força .
Passo 2
Inicalmente, é pedido para determinarmos a taxa de aumento na velocidade devido a força , ou seja, a aceleração gerada por essa força.
Essa força é tangencial ao movimento, portanto gerará uma aceleração tangencial também.
Utilizando a Equação do Movimento, temos que
Passo 3
Agora descobriremos o ângulo .
Sabemos que
Portanto, para :
O valor de encontrado é de