Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 103
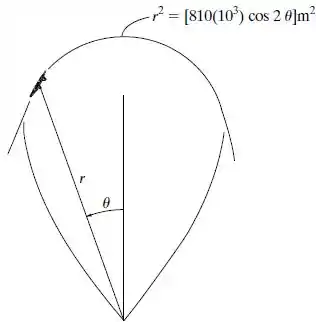
Um avião executa o loop vertical definido por . Se o piloto mantém uma velocidade constante ao longo da trajetória, determine a força normal que o assento exerce sobre ele no instante que . O piloto tem massa de 75 kg.
Passo 1
O Problema nos deu as seguintes informações:
Massa do piloto:
Velocidade constante:
A questão pede para determinarmos a força normal exercida pelo assento sobre o piloto quando .
Desenhamos o seguinte diagrama de corpo livre:
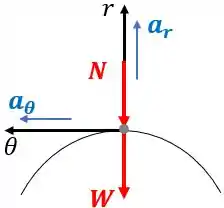
Onde é a força peso e ;
Passo 2
Sabemos que a trajetória é definida por
Para
Derivando em relação a em ambos os lados, obtemos
Derivando novamente em relação a em ambos os lados, temos que
Passo 3
As componentes radial e transversal da velocidade são dadas por
Sabemos que e, analisando o resultado acima, vemos que a componente radial de é nula, portanto
Substituindo esse resultado em , obtemos
Passo 4
Sabemos que as componentes da aceleração nas coordenadas e são dadas por
Logo,
Passo 5
Aplicaremos as Equações do Movimento.
Analisando no eixo , temos que