Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 9

8.9. Se o coeficiente de atrito estático em todas as superfícies de contato for μ s , determine a inclinação θ em que os blocos idênticos, de peso W cada um, começam a deslizar.

Passo 1

Vamos começar desenhando os diagramas de corpo livre.

Podemos separar a analise em 2 casos, o primeiro caso a gente trata do peso de cima, onde o que impede ele de deslizar é o contato com o peso de baixo. E o segundo caso é o peso que está em baixo.

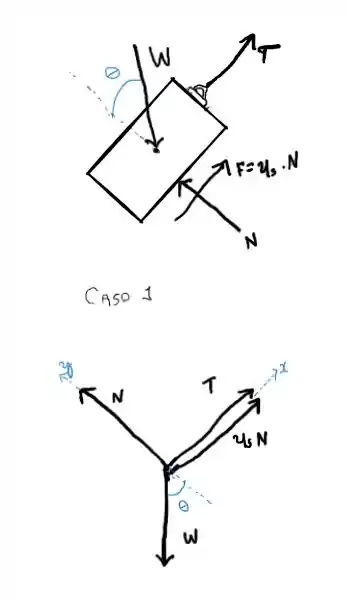
E para o caso 2

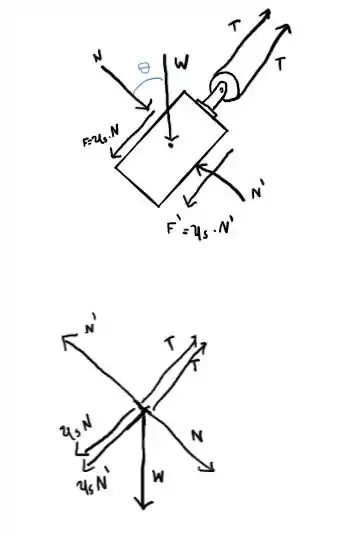
Passo 2

Agora vamos usar as equações de equilíbrio, para o primeiro caso temos

F R y = 0

F R y = N - W ⋅ cos ⁡ θ = 0

Então

N = W ⋅ cos ⁡ θ

E

F R x = 0

F R y = T + μ s ⋅ W ⋅ cos ⁡ θ - W ⋅ sin ⁡ θ = 0

Então

T = W ⋅ sin ⁡ θ - μ s ⋅ W ⋅ cos ⁡ θ

Passo 3

Agora vamos usar as equações de equilíbrio para o segundo caso temos

F R y = 0

F R y = N ' - W ⋅ cos ⁡ θ - W ⋅ cos ⁡ θ = 0

Então

N ' = 2 ⋅ W ⋅ cos ⁡ θ

E

F R x = 0

F R y = 2 ⋅ W ⋅ sin ⁡ θ - μ s ⋅ W ⋅ cos ⁡ θ - μ s ⋅ W ⋅ cos ⁡ θ - μ s ⋅ 2 ⋅ W ⋅ cos ⁡ θ - W ⋅ sin ⁡ θ = 0

Então

sin ⁡ θ - 5 ⋅ μ s ⋅ cos ⁡ θ = 0

Logo

θ = t a n - 1 ( 5 ⋅ μ s )

Resposta

θ = t a n - 1 ( 5 ⋅ μ s )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carpinteiro empurra lentamente a tábua uniforme horizontalmente sobre o topo do cavalete. A tábua tem um peso uniforme de 50N / m , e o cavalete tem um peso de 75N e centro de gravidade em G . Deter
O carpinteiro empurra lentamente a tábua uniforme horizontalmente sobre o topo do cavalete. A tábua tem um peso uniforme de 50N / m , e o cavalete tem um peso de 75N e centro de gravidade em G . Deter
Se cada caixa pesa 75k g , determine a menor força horizontal P que o homem precisa exercer na caixa de cima a fim de causar movimento. O coeficiente de atrito estático entre as caixas é μ s = 0 , 6 5
Se a garota com 35k g estiver na posição d = 1,2m , determine o coeficiente mínimo de atrito estático μ s nos pontos de contato A e B de modo que a tábua não deslize. Despreze o peso da tábua.
Se o coeficiente de atrito estático nos pontos de contato A e B é μ s = 0,4 , determine a distância mínima d onde uma garota de 35k g pode permanecer sobre a tábua sem que a tábua deslize. Despreze o