Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 52
Se os coeficientes de atrito estático nos pontos de contato e são e , respectivamente, determine a menor força que fará com que o carrretel de tenha iminência de movimento.
Passo 1
O problema pede que descubra o menor força e o menor ângulo para começar a girar o rolo.
Beleza, a gente começar fazendo um diagrama de corpo livre pra ficar mais fácil ver:
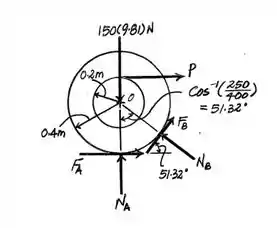
E sabemos que os equilíbrios são calculados por:
Passo 2
Agora, vamos pegar as forças que tão atuando na direção horizontal:
E na direção vertical:
E por último o momento, e a gente pega o centro como eixo de rotação:
Passo 3
Calma, tá quase acabando, basta resolver o sistema de equações:
Dica: começa somando a primeira com a última equação para eliminar .
E depois de resolver o sistema vamos encontrar:
Resposta
Exercícios de Livros Relacionados
A viga A B tem massa e espessura desprezíveis e está sujeita a uma carga distribuída triangular. Ela é apoiada por um pino em uma ponta e por um poste com massa de 50k g e espessura desprezível na out
Determine a força de atrito na caixa de 40k g e a força normal resultante em sua posição x , medida a partir do ponto A , se a força é P=300N . Considere μ s = 0,5 e μ k = 0,2 .
O gancho por atrito é composto de uma estrutura fixa e de um cilindro de peso desprezível. Um pedaço de papel é colocado entre a parede e o cilindro. Se θ=20 º º, determine o menor coeficiente de atri
O disco tem peso W e encontra-se em um plano que possui coeficiente de atrito estático m. Determine a maior altura h à qual o plano pode ser elevado sem fazer com que o disco deslize.
O semicilindro homogêneo tem massa de 20k g e centro de massa em G. Se a força P é aplicada na borda, e r=300m m , determine o ângulo θ quando o semicilindro está na iminência de deslizamento. O coefi