A viga tem massa e espessura desprezíveis e está sujeita a uma carga distribuída triangular. Ela é apoiada por um pino em uma ponta e por um poste com massa de e espessura desprezível na outra. Determine os dois coeficientes de atrito estático, em e em , de modo que, quando a intensidade da força aplicada for aumentada para , o poste deslize em e simultaneamente.
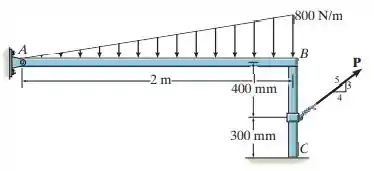
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.
Primeiramente, devemos determinar o coeficiente de atrito máximo, para isso, vamos utilizar a segunda lei de Newton no membro , temos:
Passo 2
Agora, basta fazer o mesmo para todos os elementos das vigas a fim de determinarmos os dois coeficientes de atrito estático, em e em , de modo que, quando a intensidade da força aplicada for aumentada para , o poste deslize em e simultaneamente:
Assim, o coeficiente de atrito estático em vai ser:
E o coeficiente de atruti estático em vai ser:
Resposta
Sim, o homem conseguirá mover a caixa.