Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas fundamentais - Ex. 21
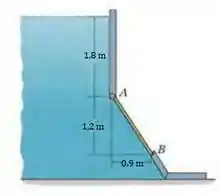
Determine a intensidade da força hidrostática atuando sobre a comporta , que tem uma largura de . O peso específico da água é .
Passo 1
Fala, querido! A gente quer a força resultante causada pelo fluído na barragem. Aí a gente precisa lembrar que o carregamento causado por um fluído tem cara de triângulo, assim:
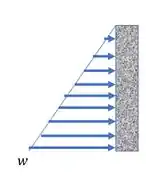
Nosso problema, é que temos uma parte vertical da parede e uma parte inclinada. Mas calma, vamos conseguir porque somos persistentes.
Na nossa situação, ainda podemos desenhar esse triângulo. Só temos que ter atenção a alguns detalhes:
- vai ser o valor do carregamento no fundo
- a ponta do triângulo precisa estar na face do líquido, ou seja, no nível da água.
- um dos catetos do triângulo precisa estar paralelo e coladinho na parede onde a gente quer calcular a resultante.
Percebe que tudo isso acontece na imagem acima, e vai acontecer aqui também se pensarmos assim:
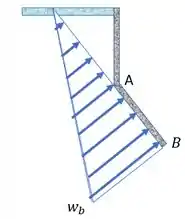
Repara que o carregamento (as setinhas) está perpendicular sobre a parede , porque queremos a resultante nela. E a pontinha do triângulo está no nível da água.
Só mais uma observação para acabar, nós só queremos a força resultante em , então só olhamos o carregamento que está sobre esse segmento:
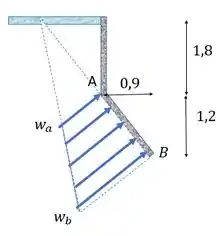
Aí o que a gente precisa fazer é achar a força resultante desse carregamento em forma de trapézio. Bora lá!
Passo 2
Sabemos que a barragem tem metro de largura, certo? Tendo isso em mente, vamos descobrir a intensidade de carga que a água causa na barragem nos pontos e :
Esse vai ser o valor de na profundidade de ,
Esse vai ser o valor de na profundidade de ,
Passo 3
A força resultante da água na barragem pode ser escrita como a área do trapézio que representa o carregamento. Assim,
onde é o tamanho do trecho . Através do teorema de pitágoras, podemos descobrir o valor dele! Assim,
Logo, a força é igual a:
Resposta
A força hidrostática é igual a: