Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 19.Problemas - Ex. 15

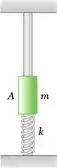
Um colar de 5 kg repousa sobre a mola mostrada na figura, à qual não está preso. Observa-se que quando o colar é empurrado 180 mm ou mais para baixo e liberado, ele perde contato com a mola. Determine (a) a constante da mola, (b) a posição, a velocidade e a aceleração do colar 0,16 s após ter sido empurrado 180 mm para baixo e liberado.

Passo 1

O enunciado pede que a gente Determine (a) a constante da mola, (b) a posição, a velocidade e a aceleração do colar 0,16 s após ter sido empurrado 180 mm para baixo e liberado

  1. x = x m sin ⁡ ω n t + ϕ

    x 0 = x m sin ⁡ 0 + ϕ = 0.180   m

    x ˙ 0 = 0 = x m cos ⁡ 0 + ϕ

    ϕ = π 2

    x m = 0.180   m

    x = 0.180 sin ⁡ ω n t + π 2

    Passo 2

    Quando o colar acaba de sair da mola, sua aceleração é g ↓ e v = 0.

    x ˙ = 0.180 ω n cos ⁡ ω n t + π 2

    v = 0                 0 = 0.180 ω n cos ⁡ ω n t + π 2

    ω n t + π 2 = π 2

    a = - g = - 0.180 ω n 2 sin ⁡ ω n t + π 2

    - g = - 0.180 ω n 2                 ω n = 9.81   m/ s 2 0.180   m

    ω n = 7.382   rad/s

    ω n = k m

    k = m ω n 2 = 5   kg 7.382   rad/s 2 = 272.5   N/m

    Passo 3

ω n = 7.382   rad/s

x = 0.180 sin ⁡ 7.382 t + π 2

Em t = 0.16 s:

Posição.

x = 0.180 sin ⁡ 7.382 0.16 + π 2 = 0.06838

Velocidade.

x ˙ = 0.180 7.382 cos ⁡ 7.382 0.16 + π 2 = - 1.229   m/s

Aceleração.

x ¨ = - 0.180 7.382 2 sin ⁡ 7.382 0.16 + π 2 = - 3.726   m/ s 2

Resposta

a )   k = 273   N/m

b )   x = 68.4   mm posição abaixo do equilíbrio

v = 1.229   m/s ↑

a = 3.73   m/ s 2  ↑

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O berço de 9 kg é apoiado conforme mostrado por dois discos uniformes que rolam sem deslizar em todas as superfícies de contato. A massa de cada disco é m = 6 kg e o raio de cada disco é r = 80 mm. Sa
Duas hastes estreitas idênticas AB e BC são soldadas para formar um conjunto em forma de L. O conjunto é pressionado contra uma mola em D e liberado da posição mostrada. Sabendo que o ângulo máximo de
O movimento da haste AB de 10 kg delgada é guiado por colares de massa desprezível que deslizam livremente nas hastes verticais e horizontais mostradas. Sabendo que a barra é liberada do repouso quand
Resolva o problema 17.25, assumindo que o cilindro é substituído por um tubo de parede fina de raio r e massa m.17.25 - Uma corda é enrolada em torno de um cilindro de raio r e massa m, conforme mostr
As extremidades de uma haste AB de 9 lb são restritas a se mover ao longo de fendas cortadas em uma placa vertical, como mostrado. Uma mola de constante k = 3 l b / i n . é fixado à extremidade A de t