Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 19.Problemas - Ex. 40

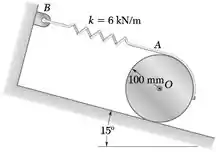
Uma barra AB de 7,5 kg está aparafusada a um disco uniforme de 6 kg como mostrada na figura. Uma esteira é presa na borda do disco e uma mola que mantém a barra em repouso na posição mostrada na figura. Se a extremidade A da barra é movida 20 mm para baixo e liberada, determine (a) o período de vibrações, (b) a máxima velocidade da extremidade A.

Passo 1

O enunciado pede que a gente encontre (a) o período de vibrações, (b) a máxima velocidade da extremidade A

Equação de movimento.

+   Σ M B = Σ M B eff :             m g L 2 cos ⁡ θ - k x r = I A B α + m α L 2 L 2 + I Disco α

onde x = r θ + δ ST e das estatísticas,

m g L 2 = k δ ST r

Passo 2

Supondo ângulos pequenos cos ⁡ θ ≈ 1 , Equação (1) torna-se

m g L 2 θ - k r 2 θ - k r δ ST = I A B + m L 2 2 + I Disco α

I A B + m L 2 4 + I Disco θ ¨ + k r 2 θ = 0

Passo 3

Dados:

m = 15 32.2 = 0.46584   lb ∙ s 2 /ft

m disco = 12 32.2 = 0.37267   lb ∙ s 2 /ft

L = 36   in. = 3.0   ft

r = 10   in . = 0.83333   ft

k = 30   lb/in. = 360   lb/ft

I A B = 1 12 m L 2 = 1 12 0.46584 3.0 2 = 0.34938   lb ∙ s 2 /ft

I Disco = 1 2 m Disco r 2 = 1 2 0.37267 0.83333 2 = 0.1294   lb ∙ s 2 /ft

0.34935 + 1 4 0.46584 3.0 2 + 0.1294 θ ¨ + 360 0.83333 2 θ = 0

1.5269 θ ¨ + 250 θ = 0                 ou                 θ ¨ + 163.73 θ = 0

Passo 4

  1. Frequência natural e período.

    2. ω n 2 = 163.73   rad/s 2

    ω n = 12.796   rad/s

    τ = 2 π ω n = 2 π 13.076

    τ = 0.491   s

    Passo 5

  2. Velocidade máxima.

v m = ω n x m = 12.796 0.75

v m = 9.60   in/s

Resposta

a )   τ = 0.491   s

b )   v m = 9.60   in/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento angular H D do disco do Problema 18.6 sobre o Ponto D.
Um disco homogêneo de massa me raio r é montado no eixo vertical AB. A normal para o disco em G forma um ângulo, β = 25 ∘ com o eixo. Sabendo que o eixo tem uma velocidade angular constante w, determi
Uma barra de seção transversal uniforme é usada para formar o eixo mostrado. Denotando por m a massa total do eixo e sabendo que o eixo gira com uma velocidade angular constante ω , determine (a) o mo
A placa triangular mostrada na figura tem uma massa de 7,5 kg e está soldada a um eixo vertical AB. Sabendo que a placa gira à taxa constante 12 rad/s, determine a quantidade de movimento angular em r
A placa triangular mostrada na figura tem uma massa de 7,5 kg eestá soldada a um eixo vertical AB. Sabendo que a placa gira à taxaconstante 12 rad /s, determine a quantidade de movimento angular em re