Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 25
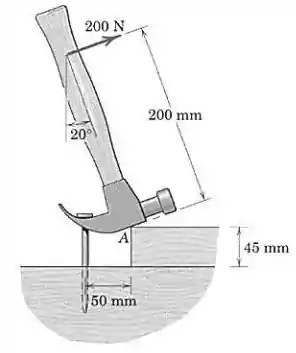
A colocação de um bloco sob a cabeça de um martelo, como mostrado, facilita muito a extração do prego. Se um puxão de no cabo do martelo for necessário para puxar o prego, calcule a força trativa no prego e o módulo da força exercida pela cabeça do martelo no bloco. As superfícies de contato em são suficientemente ásperas para prevenir escorregamento.
Passo 1
Vamos considerar as forças que atuam no martelo, que causam momento em torno do ponto de contato . A força de causa momento no sentido horário (negativo) e a força trativa atua no martelo para baixo, causando momento no sentido anti-horário (positivo):
Passo 2
Através do equilíbrio de forças na horizontal, descobrimos a componente da força atuando em :
Fazemos o mesmo na direção vertical para obter :
Logo, o módulo da força atuando no ponto deve ser: