Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 88
Determine as componentes horizontal e vertical da reação do pino A e a força no cabo BC. Despreze a espessura dos membros
Passo 1
Falaa! Queremos as reações em e a tensão em .
Bem estamos em equilíbrio então as forças verticais, horizontais e momentos se anulam
Esse é um problema com algumas nuances, se olhar rápido pode perder. Vamos só entender o que está acontecendo.
A peça horizontal recebe uma carga distribuída. A gente pode substituir essa carga por uma força concentrada. O valor dessa força é a área desse triângulo que representa a carga, ou seja
Achei P1 calculando a área do triângulo tendo altura 200 e base 4,5. E P1 está localizado na linha que passa pelo centroide do triângulo, e isso acontece a 1/3 do comprimento a partir da base ou seja
P2 está já mostrado na figura do problema, então P2 = 100N
Vamos dar uma olhada no diagrama de forças
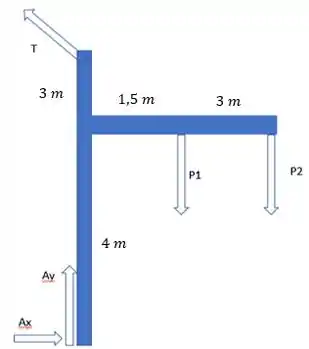
E a corda BC faz uma tração (T) no topo dessa coluna. Além disso o Pino A vai segurar qualquer forma de movimento. Então ele vai participar de todas as contas.
Bora lá!
Passo 2
Vamos definir uma orientação antes de começar. Gosto sempre de trabalhar em sentido horário. Essa orientação é arbitrária, se você estiver feito no sentido contrário, beleza! Só ao conferir as contas os sinais estarão trocados.
Então vamos lá. Tudo o que fizer meu sistema tentar rodar em Horário é ( + ), tudo o que tentar fazer tentar rodar em sentido contrário é ( - ),
Outra coisa. Quando fazemos momento temos que olhar para o PAR distância e força. Elas têm que ser ortogonais. Show! Vamos cair dentro.
Passo 3
Vamos fazer o somatório de momentos em :
Antes vamos entender que se a gente decompor a Tração em Tx e Ty. Vamos ver que a parte Tx ( projeção no eixo x ) também ajuda a tentar rotacionar o sistema. E então ele vai entrar para nossa conta de momento. Já Ty não entra porque sua linha de ação passa por
Lembrando que como essa força está na horizontal, então o par dele de distancia vai ser com a vertical.
Passo 4
Para o somatório de forças, consideramos para cima positivo e para direita positivo.
Prontinho 😊