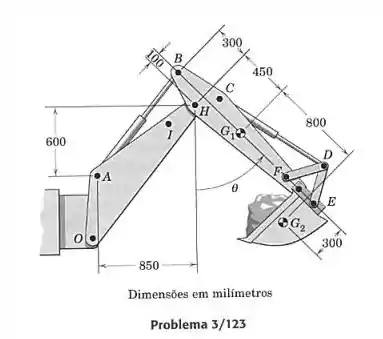
As principais características de uma pequena retroescavadeira estão mostradas na ilustração. O elemento (completo, com o cilindro hidráulico e as hastes de controle da caçamba e ) tem uma massa de 200 kg, e um centro de massa em . A caçamba e sua carga de argila tem uma massa de 140 kg e um centro de massa em . Para determinar as características do projeto operacional da retroescavadeira, determine a força no cilindro hidráulico em função da posição angular do elemento e faça um gráfico na faixa . Para que valores de a força se anula? O elemento é fixo para esse exercício; observe que seu cilindro hidráulico de controle (não mostrado) vai de um ponto próximo a até o pino . Semelhantemente, o cilindro hidráulico de controle da caçamba é mantido em um comprimento fixo.
Passo 1
Para entender melhor a física do problema, vamos tentar representar em diagrama de corpo livre o corpo que devemos analisar. Temos o elemento junto com a caçamba sofrendo os pesos em e :
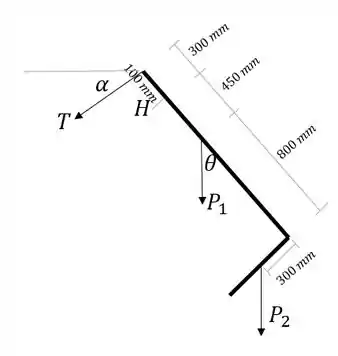
Devemos ter o momento total em torno do ponto H igual a zero.
Passo 2
Primeiro vamos calcular os momentos causados pelos pesos e . Ambos os momentos são horários, então serão negativos no eixo (sentido convencional, com para a direita, para cima e para fora do papel). A distância horizontal de até é:
A distância entre e é:
Então:
Agora só falta calcular o momento causado por .
Passo 3
Vamos calcular por um enforque vetorial. Temos:
Onde é o vetor unitário que indica a direção de . Vamos primeiro calcular :
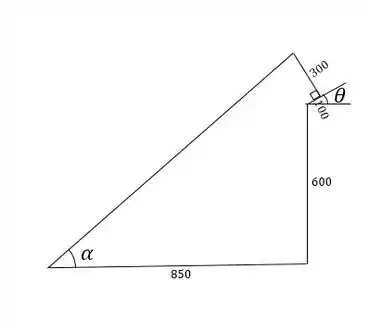
Como vemos na figura:
Agora vamos calcular o módulo desse vetor:
Agora encontramos então o vetor unitário :
Então:
Passo 4
Pronto, agora que temos as componentes de calculamos o momento em torno de . A distância horizontal entre e é:
E a distância vertical:
O momento causado pelas duas componentes é anti-horário (positivo). Então:
Passo 5
Agora, queremos somar os momentos e igualar a zero para encontrar :
Como é sepre positivo, será zero quando for zero. Então:
É o ângulo que faz a tração ser zero.