Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 10.Problemas - Ex. 128

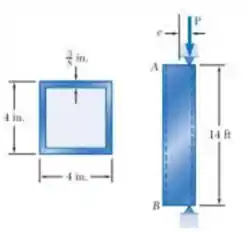
Uma coluna com 14   f t de comprimento efetivo consiste em um segmento tubular de aço com a seção transversal mostrada. Utilizando o método das tensões admissíveis , e se (a) P = 55   k i p s ,(b) P = 35   k i p s .Utilizando σ E = 36   k s i e E = 29   ×   10 6   p s i

Passo 1

Então gurizada, vamos começar logo?! iniciemos:

E = 29,000

Transição L / r : 4,71 E σ Y = 133,68

b o =   4,0   i n b i = b o - 2 t = 3,25   i n c = 2,0   i n

A = b o 2 - b i 2 = 5,4375   i n 2 I = 1 12 b o 4 - b i 4 = 12,036   i n 4

r = I A = 1,4878   i n L e = 14   f t = 168   i n

L e r = 168 1,4878 = 112,92 < 133,68

σ e = π 2 E L e r 2 = π 2 ( 29,000 ) ( 112,92 ) 2 = 22,447   k s i

σ t o t a l = σ c r 1,67 = 1 1,67 0,65 8 38 / 22,447 ( 36 ) = 11,017   k s i

P t u d o A + p t u d o e c I = σ t u d o p t u d o e c I = σ t u d o = P t u d o A e = I c P t u d o σ t u d o - P t u d o A

Passo 2

(a) P t u d o = 55   k i p s

e = 12,036 ( 2,0 ) ( 55 ) 11,017 - 55 5,4375 e = 0,0987   i n

(b) P t u d o = 35   k i p s

e = 12,036 ( 2,0 ) ( 35 ) 11,017 - 35 5,4375 e = 0,787   i n

Resposta

(a)   0,0987   i n

(b) 0,787   i n .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando as equações AISC, selecione no Apêndice B a coluna de aço estrutural A-36 de menor peso que tenha 4,2 m de comprimento e suporte uma carga axial de 200 kN. As extremidades estão engastadas.
Determine o maior comprimento de uma coluna W150 × 22 de aço estrutural A-36, se for suportada por pinos e estiver sujeita a uma carga axial de 350 kN. Use as equações AISC.
A haste de 50 mm de diâmetro é usada para suportar uma carga axial de 40 kN. Determine seu maior comprimento admissível L, se for feita de alumínio 2014-T6. Considere que as extremidades estão acoplad
A haste de 50 mm de diâmetro é usada para suportar uma carga axial de 40 kN. Determine seu maior comprimento admissível L, se for feita de alumínio 2014-T6. Considere que as extremidades estão engasta
Determine o maior comprimento de uma seção W200 × 46 de aço estrutural A-36, se for suportada por pinos e estiver sujeita a uma carga axial de 90 kN. Use as equações AISC.