Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 7

  1. Sabendo que σ a d m = 160   M P a e τ a d m = 100   M P a selecione o perfil de mesa larga mais econômico que deverá ser utilizado para suportar carga mostrada. (b) Determine os valores a serem esperados para σ m , τ m e a tensão principal σ m á x na junção da mesa com a alma de perfil selecionado.

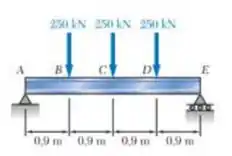
Passo 1

Então gurizada, vamos começar logo?! iniciemos com algumas conversões:

160   M P a = 24   k s i 100   M P a = 14,5   k s i

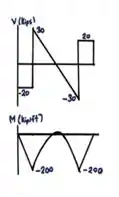
Vamos aos cálculos:

R A = 50   k i p s   ↑ R D = 50   k i p s   ↓ V m a x = 30   k i p s

M m a x = 200   k i p s × f t = 2400 × k i p × i n S m i n = M m a x σ t u d o = 2400 24 = 100   i n 3

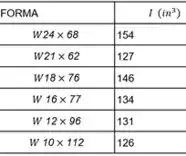
Passo 2

Usaremos W 21 × 62

d = 21,0   i n t f = 0,615   i n t w = 0,400   i n

Teremos: σ m = M m a x S = 2400 127 = 18,8976   k s i

σ m = 18,9   k s i = 130,32   M P a

Passo 3

τ m = V m a x d t w = 30 ( 21,0 ) ( 0,400 ) = 3,5714   k s i

τ m = 3,57   k s i = 24,61   M P a

c = 1 2 d = 21,0 2 = 10,50   i n y b = c - t f = 10,50 - 0,61 5 = 9,8850   i n

σ b = y b c σ m = 9,8850 10,50 ( 18,8976 ) = 17,7907   k s i

R = σ b 2 2 + τ m 2 = ( 8,8954 ) 2 + ( 3,5714 ) 2 = 9,5856   k s i

σ m a x = σ b 2 + R = 8,8954 + 9,5856 = 18,4810   k s i

σ m a x = 18,48   k s i = 127,42   M P a

Resposta

Muito bem turminha, nossa resposta para esta é W   21 × 62 ; σ m = 18,9   k s i = 130,32   M P a ; τ m = 3,57   k s i = 24,61   M P a e σ m a x = 18,48   k s i = 127,42   M P a .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14. O estado de tensão em um ponto é mostrado no elemento. Determine:(a) as tensões principais e (b) a tensão de cisalhamento máxima no plano e a tensão normal média no ponto. Especifique a orientação
15. O estado de tensão em um ponto é mostrado no elemento. Determine:(a) as tensões principais e (b) a tensão de cisalhamento máxima no plano e a tensão normal média no ponto. Especifique a orientação
13. O estado de tensão em um ponto é mostrado no elemento. Determine:(a) as tensões principais e (b) a tensão de cisalhamento máxima no plano e a tensão normal média no ponto. Especifique a orientação
16. O estado de tensão em um ponto é mostrado no elemento. Determine:(a) as tensões principais e (b) a tensão de cisalhamento máxima no plano e a tensão normal média no ponto. Especifique a orientação
18. A barra de aço tem espessura de 12 mm e está sujeita à carga periférica mostrada na figura. Determine as tensões principais desenvolvidas na barra.