Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 127

A coluna de aço tem comprimento de 5 m e é livre no topo e engastada na base. Se a área da seção transversal tiver as dimensões mostradas na figura, determine a carga crítica. e = 200 G P a e σ y = 360 M P a .

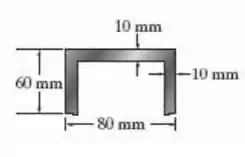
Passo 1

Como está engastada em uma extremidade e livre na outra, k = 2 .

Primeiramente, calculando-se o y do centróide e a área, teremos:

y = 2 10 × 50 25 + 80 × 10 55 2 10 × 50 + 80 × 10 = 38,333 m m

A = 2 10 × 60 + 10 × 60 = 1800 m m ²

Agora, vamos calcular o momento de inércia em x:

2 10 × 50 2 12 + 10 × 50 × 13,333 2 + 80 × 10 3 12 + 80 × 10 × 16,667 2 = 615000

Logo, calculando-se a carga crítica:

P c r = π 2 E I x k L 2

Substituindo, teremos:

P c r = 12,14 k N

Passo 2

Precisamos verificar se ocorre o escoamento:

σ c r = P c r A = 12139,6 1800 = 6,74 M P a

Logo, é menor que a tensão de escoamento.

Resposta

P c r = 12,14 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A coluna está apoiada em B e esse apoio não permite rotação, mas sim deflexão vertical. Determine a carga crítica para EI constante.
Considere uma coluna ideal com ambas as extremidades engastadas. Mostre que a carga crítica é dada por P c r = 4 π 2 E I L 2 .
Considere que a coluna está em gastada na base e no topo. Determine a carga excêntrica máxima P que pode ser aplicada sem provocar flambagem ou escoamento da coluna. E m = 12 G P a e σ y = 56 M P a .
A coluna ideal tem peso w e permanece na posição horizontal quando sujeita a uma carga axial P. Determine o momento máximo no ponto médio do vão da coluna. EI é constante.
Considere que a coluna está em gastada na base e presa por pinos no topo. Determine a carga excêntrica máxima P que pode ser aplicada sem provocar flambagem ou escoamento da coluna. E m = 12 G P a e σ