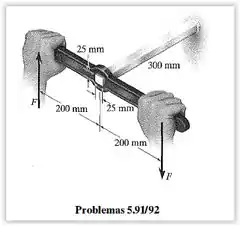
O eixo de aço tem de comprimento e é parafusado em uma parede com uma chave de torque. Determine as maiores forças conjugadas que podem ser aplicadas ao eixo sem provocar o escoamento do aço.
Passo 1
Mãos à obra, galerinha!
Então, o problema pede que determinemos as maiores forças conjugadas que podem ser aplicadas ao eixo sem provocar o escoamento do aço, sendo que a tensão de escoamento é:
O primeiro passo é calcular o torque aplicado ao eixo pela chave de torque.
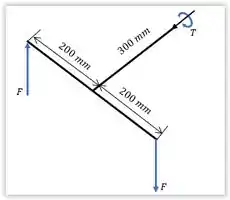
Observando a figura, notamos que ele age no sentindo horário. Pelo diagrama de corpo livre, temos:
Passo 2
Vamos descobrir o valor das forças substituindo o torque na fórmula na tensão de cisalhamento. Como a seção transversal do eixo é quadrada, temos que:
Em que é a aresta do quadrado e corresponde a , ou seja, .
Substituindo: