Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 48
Considere que a coluna está em gastada na base e presa por pinos no topo. Determine a carga excêntrica máxima P que pode ser aplicada sem provocar flambagem ou escoamento da coluna. e
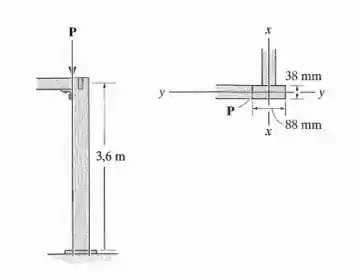
Passo 1
Para o eixo y, teremos:
Conferindo se a força não causa o escoamento:
Passo 2
Já para o eixo x:
Sabemos que:
Logo, aplicando-se a fórmula, teremos:
Esta equação não é tão simples de resolver, mas como não é nosso foco aqui, utilizaremos um programa para resolvê-la. Isolando-se
Calculando P:
Como devemos escolher o menor P, teremos:
Resposta
Exercícios de Livros Relacionados
Um tubo estrutural com a seção transversal retangular mostrada é utilizado como coluna com comprimento de flambagem de 5m. Sabendo que σ Y = 250M P aeE = 200G P a , utilize o método das tensões admiss
Uma coluna de comprimento flambagem de 4,6m deve suportar uma força centrada de 525k N . Usando o método de tensão admissível selecione o perfil de mesa larga de 200m m de altura nominal que deve ser
Duas cantoneiras de 89m m×64m m são soldadas como mostra a figura, para formarem uma coluna de flambagem de 2,4m para suportar uma força centrada de 180k N . Sabendo que as cantoneiras disponíveis t
Uma coluna de comprimento flambagem de 685,8m m deve suportar uma força centrada central de 1821k N . Usando o método de tensão admissível selecione o perfil de mesa larga de 360m m de altura nominal
Uma coluna de comprimento flambagem de 17f t deve suportar uma força centrada central de 235k i p s . Usando o método de tensão admissível selecione o perfil de mesa larga de 10i n de altura nominal q