Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 36b
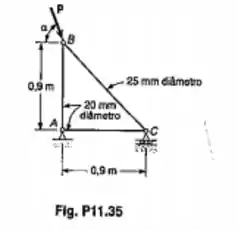
Para a estrutura do Prob. 11.35, determinar(a) o ângulo para que o coeficiente de segurança, e relação a flambagem seja máximo;(b) O correspondente coeficiente de segurança para P=7120N.
Passo 1
Fala aí, bora pra esse item b.?
O problema pede o fator de segurança para , aqui vamos calcular as reações de apoio e analisar as barras comprimidas que sofrem flambagem e relacionar o peso admissível nas barras com o peso dado, e também agora com o ângulo encontrado no item a que é .
E o peso crítico é dado por:
Precisamos encontrar as relações entre P e as reações de apoio pois P causa a flambagem indiretamente. Vamos desenhar o diagrama de corpo livre e analisar nossa situação.
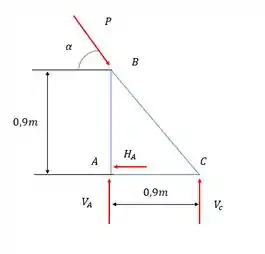
Vamos analisar somente as barras comprimidas, é valido dizer que a barra AB não corre risco de flambagem, visto que foi avaliado no item a. que para seu fator de segurança tende ao infinito, e não depende do valor de P. Então nesse caso vamos apenas buscar uma relação para
Passo 2
Vamos calcular as reações, a gente pode começar pegando o ponto A e fazendo o somatório dos momentos com o sentido horário positivo, mas antes é bom observar que P pode ser decomposto em duas direções:
Onde:
E:
Então:
Para avaliar o que rola na barra BC é preciso calcular a força. Como o triângulo possui dois lados iguais podemos afirmar que o ângulo da barra é
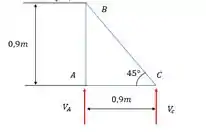
E daqui a gente pode fazer a seguinte relação:
E substituindo:
Passo 3
Temos enfim que o peso admissível é o peso que resiste a flambagem com o fator de segurança, então vamos considerar para cada barra a seguinte relação:
E:
E também:
E como a seção é circular temos:
E o comprimento da barra a gente tira fazendo Pitágoras:
E aí:
Sendo assim temos:
E como calculamos:
E enfim:
E substituindo o valor de P e encontrado no item a, temos: