Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 39
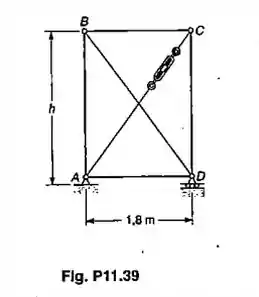
Os membros AB e CD são de barras de aço com 30mm de diâmetro. Quando o esticador é apertado, o membro diagonal AC torna-se tracionado.
Sabendo-se que um coeficiente de segurança em relação a flambagem de 3,2 é desejado, determinar a maior tração admissível em AC, quando h=2,4m
Usar E=200GPa e considerar somente a flambagem no plano da estrutura.
Passo 1
Fala aí, bora analisar essa estrutura?
Bom aqui a gente precisa analisar o comportamento da estrutura, o enunciado disse que a barra AC será tracionada então ela não sofre flambagem, porém a tração nela puxar e comprimir outras barras e é ai que a gente vai analisar a flambagem. Vamos desenhar o nó C e analisar o equilíbrio.
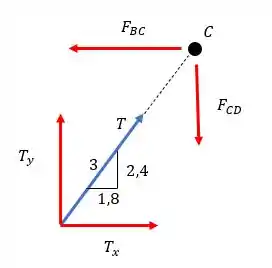
Detalhe que na figura foi desenhado o triângulo do enunciado de forma reduzida e a hipotenusa foi calculada fazendo Pitágoras com as dimensões mostradas. Essas forças nas barras serão o peso admissível que é relacionado ao fator de segurança da seguinte forma:
Lembrando que pro peso crítico é dado por:
Vamos então relacioná-las com a tração na barra AC, e avaliar qual a maior tração admissível!
Passo 2
Como prometido vamos pra nossa relação fazendo o somatório das forças no nó C:
E pela figura a gente vê que:
Daí:
E pelo somatório das forças horizontais temos:
E pela figura:
Então:
Passo 3
Bacana, encontrados os esforços podemos pensar o seguinte se essas barras resistem a flambagem com o coeficiente de segurança desejado temos que:
Então vamos ao cálculo do peso crítico.
E precisamos do momento de inércia que para seção circular é dado por:
E da figura a gente vê que o comprimento da barra BC é:
Substituindo temos:
Daí voltando ao peso admissível:
E como vimos que:
Podemos substituir e isolar T:
Passo 4
Ainda não acabou por aí, precisamos avaliar a barra CD. Faremos como no passo 3.
Então vamos ao cálculo do peso crítico.
E o momento de inércia é o mesmo pois as barras possuem o mesmo diâmetro:
E da figura a gente vê que o comprimento da barra CD é:
Substituindo temos:
Daí voltando ao peso admissível:
E como vimos que:
Podemos substituir e isolar T:
E enfim:
E como essa tração é a menor entre as duas fica sendo a tração que faz a estrutura possuir o coeficiente de segurança desejado.