Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 31
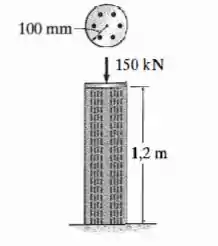
A coluna é construída de concreto de alta resistência e seis hastes de reforço de . Se ela for submetida a uma força axial de determine a tensão normal média no concreto e em cada haste. Cada uma tem diâmetro de .
Passo 1
Desejamos encontrar a tensão normal média para o concreto e para o aço nas haste, dessa forma devemos lembrar que os valores dos módulos de elasticidade para esses materiais são tabelados e dados por: . Para que a estrutura seja bem compatível, devemos ter que o alongamento do concreto deve ser igual ao do aço e assim teremos
Passo 2
Tomando a equação acima podemos fazer
Onde . Além disso, das equações de equilíbrio nós temos
Resolvendo o sistema composto pelas equações vamos obter
Passo 3
Por fim, basta substituirmos na fórmula da tensão normal e vamos obter