Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 25

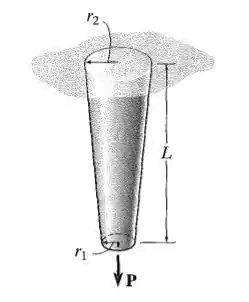
Resolva o Problema 4.24 incluindo P e o peso do material e também considerando que o peso específico da haste é γ (peso por unidade de volume).

Passo 1

O exercício pede para que nós resolvamos o problema 4.24 que pedia para mostrarmos que o deslocamento da extremidade em razão da carga P e desconsiderando o peso do material era dado por

δ = P ⋅ L π ⋅ E ⋅ r 1 r 2

Para esse problema, vamos estar levando em consideração o peso do material dado por γ .

Passo 2

Das forças internas no material vamos ter

∑ F y = 0 → P x - w x - P = 0 → P x = P + w x

Para encontrarmos o valor de A x vamos precisar utilizar algumas coisas de geometria como semelhança de triângulos, por exemplo. Tomemos então a seguinte construção que pode ser feito com a geometria do problema

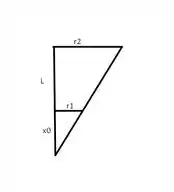
Fazendo a semelhança de triângulos vamos obter

L + x 0 r 2 = x 0 r 1 → x 0 = L ⋅ r 1 ( r 2 - r 1 )

De maneira análoga podemos fazer

r x = r 1 + r 2 - r 1 L ⋅ x = r 1 ⋅ L + r 2 - r 1 ⋅ x L

→ A x = π ⋅ r x 2 = π L 2 ⋅ r 1 ⋅ L + r 2 - r 1 ⋅ x 2

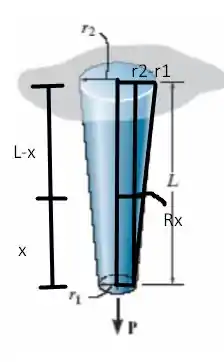
Como agora estamos levando em consideração o peso do material, vamos ter mais o seguinte termo que vai ser acrescido no resultado final

w x = γ 3 ⋅ A x ⋅ x 0 + x - γ π 3 ⋅ r 1 2 ⋅ ( x 0 )

→ w x = γ ⋅ π 3 L 2 ⋅ ( r 2 - r 1 ) ⋅ r 1 ⋅ L + r 2 - r 1 ⋅ x 3 - r 1 3 ⋅ L 3

Passo 3

Agora só resolvermos a integral que é dada por

δ 1 = ∫ 0 L w x A x ⋅ E = γ ⋅ π 3 E ⋅ ( r 2 - r 1 ) ⋅ ∫ 0 L r 1 ⋅ L + r 2 - r 1 ⋅ x 3 - r 1 3 ⋅ L 3   d x r 1 ⋅ L + r 2 - r 1 ⋅ x 2

δ 1 = γ ⋅ L 2 ⋅ ( r 2 + r 1 ) 6 E ⋅ ( r 2 - r 1 ) - γ ⋅ L 2 ⋅ r 1 2 3 E ⋅ r 2 - r 1 ⋅ r 2

Sendo assim, nosso deslocamento total vai ser dado por

δ = δ 1 +   ∫ 0 L P A x ⋅ E = γ ⋅ L 2 ⋅ ( r 2 + r 1 ) 6 E ⋅ ( r 2 - r 1 ) - γ ⋅ L 2 ⋅ r 1 2 3 E ⋅ r 2 - r 1 ⋅ r 2 + P ⋅ L π ⋅ E ⋅ r 1 r 2  

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra tem área de seção transversal de 1.800m m 2 e E =250G P a . Determine o deslocamento da extremidade A da barra quando submetida ao carregamento distribuído
A haste de aço A - 36 está sujeita ao carregamento mostrado. Se a área de seção transversal da haste for 60m m 2 , determine o deslocamento de B e A . Despreze o tamanho dos acoplamentos em B ,CeD .
O eixo A C de aço A - 36 com 15m m de diâmetro é sustentado por um colar rígido fixado ao eixo B . Se for submetido a uma carga axial de 80k N em sua extremidade, determine a distribuição de pressão u
O conjunto é composto por uma haste C B de aço A - 36 e uma haste B A de alumínio 6061 - T 6 , cada uma com diâmetro de 25m m . Determine as cargas aplicadas P 1eP 2 se A se deslocar2m m para a direit
O conjunto é composto por três hastes de titânio ( T i- 6 A 1 - 4 V ) e uma barra rígida A C . A área da seção transversal de cada haste é dada na figura. Se uma força de 30k N for aplicada ao anel F