Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 24
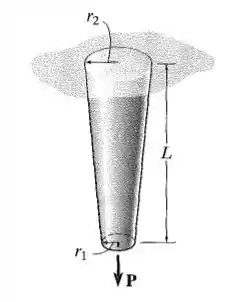
A haste tem uma leve conicidade e comprimento . Está suspensa a partir do teto e suporta uma carga em sua extremidade. Mostre que o deslocamento de sua extremidade em razão dessa carga é Despreze o peso do material. O módulo de elasticidade é .
Passo 1
Queremos mostrar que o deslocamento da extremidade em razão da carga é dado pela fórmula descrita no problema. Neste caso, podemos desprezar o peso do material. Além disso, devemos notar que esse deslocamento vai ser dado em função de uma integral e dado por
Ou seja, descobrindo quem é o nosso problema deixa de ser de resistência e passa a ser de cálculo onde necessitaremos resolver uma integral e fazer alguma manipulação algébrica.
Passo 2
Para encontrarmos o valor de vamos precisar utilizar algumas coisas de geometria como semelhança de triângulos, por exemplo. Tomemos então o seguinte desenho que pode ser feito com a geometria do problema
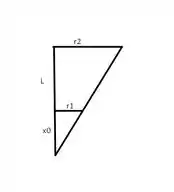
Fazendo a semelhança de triângulos vamos obter
De maneira análoga podemos fazer
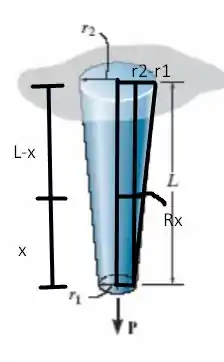
Passo 3
Precisamos, agora, apenas resolver a nossa integral mencionada no início que é
Resposta
Ei, a resposta está no passo a passo :)