Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 26
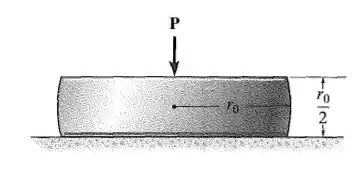
Dois lados opostos de uma esfera de raio foram cortados para fabricar o suporte apresentado na figura. Se a altura original do suporte for , determine até que distância ele se encurta quando suporta uma carga . O módulo de elasticidade é .
Passo 1
Desejamos encontrar qual o valor ao qual a altura da nossa estrutura vai se encontrar quando uma carga de módulo atingir nosso material, sendo o módulo de elasticidade igual a . Para esse caso vamos ter que esse encurtamento vai ser dado a partir de uma integral que é
Passo 2
Da geometria do problema temos a seguinte relação entre .
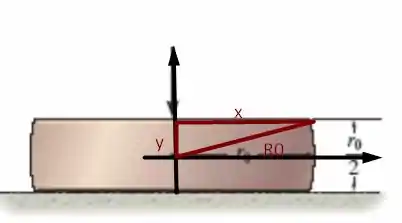
Aplicando Pitágoras no triângulo retângulo destacado vamos ter
Sendo assim, vamos ter
Passo 3
Tendo em vista que nossa altura podemos resolver a integral e obteremos
Resposta
Exercícios de Livros Relacionados
Determine o alongamento da tira de alumínio quando submetida a uma força axial de 30k N .E a l=70G P a .
O sistema articulado é composto por três elementos de aço A - 36 conectados por pinos, cada um com área de seção transversal de 500m m 2 . Se uma força vertical P=250k N for aplicada à extremidade B d
O raio do pedestal apresentado na figura é definido pela função r=2 / ( 2+y 1 2 )m , onde y é dado em metros. Se o módulo de elasticidade para o material for E=100M P a , determine o deslocamento da p
O poste é feito de abeto Douglas e tem diâmetro de 60m m . Se estiver sujeito a uma carga de 20k N e o solo proporcionar resistência ao atrito w=4k N / m uniformemente distribuída ao longo de seus lad
A viga rígida está apoiada em suas extremidades por dois tirantes de a ç oA - 36 ç . Os diâmetros das hastes são d A B=12m med c d=7,5m m . Se a tensão admissível para o aço for σ a d m=115M P a , det