Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 15

Se a viga T for submetida a um cisalhamento vertical V = 60kN, determine a força de cisalhamento vertical à qual a aba resiste.

Passo 1

Dados da questão: V = 60 k N

A questão pede: A força na aba.

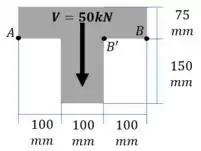
Estratégia de resolução: Para encontra a força sobre um aba devemos integrar a tensão sobre a área. Em outras palavras, vamos integrar a Equação 7.3. Nesta equação, o momento de inércia I , a base t e o cisalhamento aplicado V são contantes, mas o momento estático Q varia de acordo com a seção. Então para realizar a integração vamos precisar:

  • Calcular o centroide
  • Calcular o momento de inércia
  • Definir uma função para o momento estático
  • Integrar a força sobre a área da aba

Passo 2

Vamos começar calculando o centroide.

y c = A a m a r e l a y a m a r e l a + A v e r d e y v e r d e A a m a r e l a + A v e r d e

y c = 150 ⋅ 100 ⋅ 75 + 75 ⋅ 300 ⋅ 187,5 150 ⋅ 100 + 75 ⋅ 300

y c = 142,5   m m

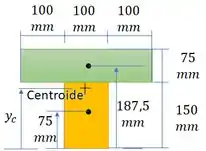
Passo 3

Agora calculamos o momento de inércia em relação ao centroide

I = I v e r d e + I a m a r e l o

I = 300 ⋅ 75 3 12 + 300 ⋅ 75 ⋅ 45 2 + 100 ⋅ 150 3 12 + 100 ⋅ 150 ⋅ 67,5 2

I = 152,57 ⋅ 10 6 m m 4

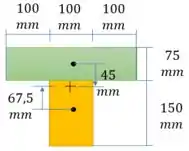
Passo 4

Vamos definir uma equação para o momento estático na aba:

Q = x ⋅ 300 ⋅ 82,5 - x 2

Q = 24750 x - 150 x 2

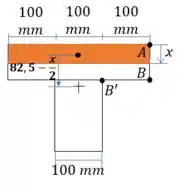
Passo 5

Bem, sabemos por definição que tensão é força sobre área. Em termos infinitesimais:

τ = d F d A

Sabemos que a tensão de cisalhamento é dada por:

V Q ( x )   I t = d F d A

Isolando d F :

d F = V Q ( x )   I t d A

Perceba que a área da seção é quadrada. Em outras palavras: d A = t ⋅ d x

Substituindo o valor de Q ( x ) temos:

d F = V I t 24750 x - 150 x 2 ⋅ t d x

Simplificando

d F = V I 24750 x - 150 x 2 ⋅ d x

Aplicando a integral:

F = V I ∫ 0 75 24750 x - 150 x 2 ⋅ d x

F = V I 12375 x 2 - 50 x 3 0 75

Aplicando os valores:

F = 60   k N 152,57 ⋅ 10 6 m m 4 [ 12375 ⋅ 75 m m 2 - 50 ⋅ 75 m m 3 ]

F = 19,08   k N

Resposta

F = 19,08   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga de perfil de aço laminado com abas largas e submetidas ao carregamento indicado, determinar numa seção localizada no ponto médio entre os pontos D e E : (a) a maior tensão normal; (b) a ma
Duas placas retangulares são soldadas a um perfil de aço laminado com abas largas, formando a viga mostrada. Determinar a maior força cortante admissível, se a tensão de cisalhamento na viga não deve
Para a viga com o carregamento indicado, considerar a seção n - n e determinar a tensão de cisalhamento no: (a) ponto a ; (b) ponto b .
Para a viga com o carregamento indicado, considerar a seção n - n e determinar a tensão de cisalhamento no: (a) ponto a ; (b) ponto b .
Determinar a maior tensão de cisalhamento, na seção n - n .