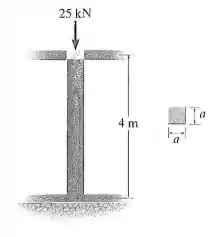
A coluna de madeira tem 4 m de comprimento e deve suportar a carga axial de 25 kN. Se a seção transversal for quadrada, determine a dimensão a de cada um de seus lados usando um fator de segurança FS = 1,5 contra flambagem. Considere que a coluna está engastada no topo e na base. Use a equação de Euler. e
Passo 1
Como está engastada nas extremidades,
Primeiramente, calculando-se o momento de inércia, teremos:
A carga crítica pode ser calculada da seguinte forma:
Sabemos que:
Substituindo os valores e isolando-se o , teremos:
Verificando-se a tensão crítica:
Como é menor que a tensão de escoamento, está ok.