Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 37
37. Determine se a estrutura pode suportar uma carga , se o fator de segurança para flambagem do elemento estrutural for . Considere que é feito de aço e que suas extremidades estão presas por pinos para flambagem no eixo e engastadas para flambagem no eixo. , .
Passo 1
Primeiro, vamos montar o diagrama de corpo livre da barra :
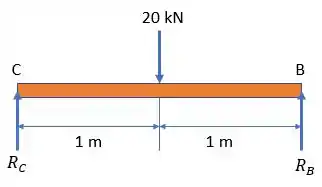
Dessa imagem, é fácil a gente ver que a reação tem o mesmo valor da reação devido à simetria do diagrama. Assim, como só há uma força de aplicada, cada reação vale .
Passo 2
Agora, vamos calcular a a força crítica pela relação com a força e o fator de segurança:
Passo 3
Aqui, vamos calcular a flambagem no eixo .
Como as extremidades estão presas por pinos, temos .
O momento de inércia no eixo , como é uma seção retangular, é dado pela fórmula:
Onde é a aresta paralela ao eixo e é a aresta perpendicular ao eixo.
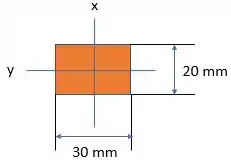
Como o valor calculado pela fórmula para é menor do que o valor calculado pelo fator de segurança, essa força não é admissível nesse eixo.
Passo 4
Agora, vamos calcular a carga para a haste .
O diagrama de corpo livre da barra:
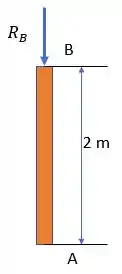
Como calculamos no Passo , .
Passo 5
Já sabemos, também, a força , que é igual a pelo fator de segurança. Agora, é só substituir os valores na fórmula:
Lembrando que o eixo está engastado, portanto .
Como o valor calculado pela fórmula para é menor do que o valor calculado pelo fator de segurança, essa força é admissível nesse eixo.
Passo 6
Vamos calcular a tensão devido à força crítica para verificar se ele ultrapassa a tensão de escoamento :
Como , a carga crítica é admissível nesse eixo.
Passo 7
E por fim, verificar pelo fator de segurança , se a carga no eixo é admissível (a qual já foi observada que não é).
Como o Fator de segurança encontrado foi menor do que o Fator de segurança fornecido, a carga não é admissível.
Resposta
Portanto, verificamos que a estrutura não pode suportar a carga com o exigido.