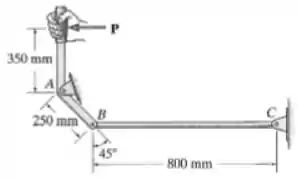
35. Determine a força máxima que pode ser aplicada ao cabo de modo que a haste de controle de aço não sofra flambagem. A haste tem diâmetro de .
Passo 1
Primeiro, a gente vai analisar a barra separadamente, ou seja, o elemento a parte do elemeto :

Agora, faremos o somatório de forças e momentos para achar as relações entre as componentes das forças e e a força :
Agora, vamos analisar o sistema como um todo, ou seja , junto com o elemento . Assim, faremos a somatória de momento em relação ao ponto :
Passo 2
Agora, vamos resolver as equações .
Para simplificar, podemos ver que não há forças atuando no sentido , portanto:
Na equação , temos:
E da equação :
Passo 3
Agora, devemos pegar a força atuante na haste para achar a força crítica :
Podemos achar a força crítica pela fórmula:
Como o exercício disse que é um aço , nós temos a seguinte característica tabelada:
Módulo de elasticidade do material
Temos que calcular também o momento de inércia , que, para seções circulares, temos a fórmula:
A medida de será o comprimento da haste que é de .
Por fim, .
Passo 4
Finalmente, a gente só tem que achar a tensão crítica pela fórmula de tensão da força crítica :
Lembrando que :
Passo 5
Sabemos que a tensão de escoamento do aço é de . Como é menor que a tensão de escoamento, a haste não sofre flambagem.
Resposta
A força que pode ser aplicada no sistema para que a haste não sofra flambagem é de: