Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 39
39. Considere que os elementos estruturais da treliça estão acoplados por pinos. Se o elemento estrutural for uma haste de aço com diâmetro de , determine o maior valor da carga que pode ser suportada pela treliça sem provocar flambagem naquele elemento estrutural.
Passo 1
E aí amiguinhos! Aqui vamos nós de novo pra mais um probleminha de flambagem!
E dessa vez, temos uma questão que mistura flambagem com treliças!
Se liga só! A questão tá pedindo pra gente o maior valor da carga que pode ser suportada pelo elemento estrutural pra não prejudicar nossa treliça e deixar ele bonitinha do jeito que tá!
Ou seja, vamos precisar obter a força nesse elemento e ver se existe alguma relação entre ela e .
Indo direto ao ponto! Vamos ter que resolver a treliça!
Depois, é só usar a fórmula abaixo da flambagem, que você já tá careca de saber...
Passo 2
Bora começar fazendo o diagrama de corpo livre pra nossa treliça! Ele vai ficar do seguinte jeitinho abaixo...
E calcularemos o somatório dos momentos em A, que vai nos dar a reação de apoio em D:
Considerando o sentido horário positivo, temos:
E com o somatório das forças em y:
Passo 3
Agora se liga nessa dica aqui, dá uma boa olhada na barra AH, ela não pode possuir esforço vertical, pois ao chegar no nó H não consegue transferir nenhum esforço. Então pra gente analisar o Nó A, vamos desconsiderar qualquer esforço vindo de AH, ok?
Desenhando a gente tem:
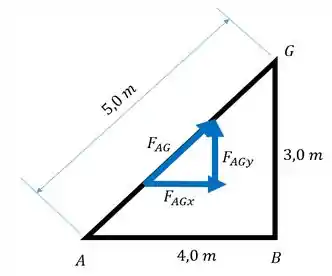
O comprimento da barra AG, foi calculado usando o teorema de Pitágoras.
Aqui a gente pode usar o somatório das forças em y, e vamos logo encontrar FAG:
Onde:
Assim:
Passo 4
Pra finalizar! Agora que já sabemos a força em função de , vamos considerar que essa vai ser a nossa forca crítica de flambagem...
E em seguida, utilizar a fórmula abaixo, que já conhecemos...
Vamos definir nossas variáveis.
Bora lá! Primeiro o comprimento de flambagem !
Bem! Cada elemento da nossa treliça tá muito bem preso por pinos em ambos os lados!
Então, temos:
E o momento de inércia da seção circular é dado por:
Uma vez que a seção tem diâmetro de , então o raio dela vai ser...
Assim:
E temos, também, por ser dado no enunciado que é um aço , o seguinte valor de módulo de elasticidade...
Pronto! Temos todos os valores que precisávamos!
Substituindo eles na fórmula da carga crítica...
E como ...
Resposta
O maior valor da força que pode ser suportada pela treliça sem provocar flambagem no elemento é de: